Advertisements
Advertisements
Question
Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. Then the value of E(X) is
(A) `37/221`
(B) 5/13
(C) 1/13
(D) 2/13
Solution
Let X denote the number of aces obtained. Therefore, X can take any of the values of 0, 1, or 2.
In a deck of 52 cards, 4 cards are aces. Therefore, there are 48 non-ace cards
 '
'
Thus, the probability distribution is as follows.
| X | 0 | 1 | 2 |
| P(X) | 1128/1326 | 192/1326 | 6/1326 |
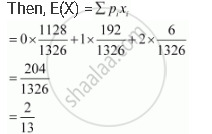
Therefore, the correct answer is D.
APPEARS IN
RELATED QUESTIONS
An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represents the number of black balls. What are the possible values of X? Is X a random variable?
An urn contains 25 balls of which 10 balls bear a mark ‘X’ and the remaining 15 bear a mark ‘Y’. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that
(i) all will bear ‘X’ mark.
(ii) not more than 2 will bear ‘Y’ mark.
(iii) at least one ball will bear ‘Y’ mark
(iv) the number of balls with ‘X’ mark and ‘Y’ mark will be equal.
Two numbers are selected at random (without replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and variance of X
Three persons A, B and C shoot to hit a target. If A hits the target four times in five trials, B hits it three times in four trials and C hits it two times in three trials, find the probability that:
1) Exactly two persons hit the target.
2) At least two persons hit the target.
3) None hit the target.
Find the probability distribution of the number of heads, when three coins are tossed.
Two cards are drawn successively without replacement from a well shuffled pack of 52 cards. Find the probability distribution of the number of aces.
Find the probability distribution of the number of white balls drawn in a random draw of 3 balls without replacement, from a bag containing 4 white and 6 red balls
From a lot containing 25 items, 5 of which are defective, 4 are chosen at random. Let X be the number of defectives found. Obtain the probability distribution of X if the items are chosen without replacement .
A fair die is tossed twice. If the number appearing on the top is less than 3, it is a success. Find the probability distribution of number of successes.
From a lot of 10 bulbs, which includes 3 defectives, a sample of 2 bulbs is drawn at random. Find the probability distribution of the number of defective bulbs.
Find the mean and standard deviation of each of the following probability distributions:
| xi : | 2 | 3 | 4 |
| pi : | 0.2 | 0.5 | 0.3 |
A discrete random variable X has the probability distribution given below:
| X: | 0.5 | 1 | 1.5 | 2 |
| P(X): | k | k2 | 2k2 | k |
Determine the mean of the distribution.
Find the mean variance and standard deviation of the following probability distribution
| xi : | a | b |
| pi : | p | q |
A fair coin is tossed four times. Let X denote the longest string of heads occurring. Find the probability distribution, mean and variance of X.
A die is tossed twice. A 'success' is getting an odd number on a toss. Find the variance of the number of successes.
A box contains 13 bulbs, out of which 5 are defective. 3 bulbs are randomly drawn, one by one without replacement, from the box. Find the probability distribution of the number of defective bulbs.
In roulette, Figure, the wheel has 13 numbers 0, 1, 2, ...., 12 marked on equally spaced slots. A player sets Rs 10 on a given number. He receives Rs 100 from the organiser of the game if the ball comes to rest in this slot; otherwise he gets nothing. If X denotes the player's net gain/loss, find E (X).
In a game, a man wins Rs 5 for getting a number greater than 4 and loses Rs 1 otherwise, when a fair die is thrown. The man decided to thrown a die thrice but to quit as and when he gets a number greater than 4. Find the expected value of the amount he wins/loses.
For what value of k the following distribution is a probability distribution?
| X = xi : | 0 | 1 | 2 | 3 |
| P (X = xi) : | 2k4 | 3k2 − 5k3 | 2k − 3k2 | 3k − 1 |
If X is a random-variable with probability distribution as given below:
| X = xi : | 0 | 1 | 2 | 3 |
| P (X = xi) : | k | 3 k | 3 k | k |
The value of k and its variance are
A departmental store gives trafnfng to the salesmen in service followed by a test. It is experienced that the performance regarding sales of any salesman is linearly related to the scores secured by him. The following data gives the test scores and sales made by nine (9) salesmen during a fixed period.
| Test scores (X) | 16 | 22 | 28 | 24 | 29 | 25 | 16 | 23 | 24 |
| Sales (Y) (₹ in hundreds) | 35 | 42 | 57 | 40 | 54 | 51 | 34 | 47 | 45 |
(a) Obtain the line of regression of Y on X.
(b) Estimate Y when X = 17.
From the following data, find the crude death rates (C.D.R.) for Town I and Town II, and comment on the results :
| Age Group (in years) | Town I | Town II | ||
| Population | No. of deaths | Population | No. of deaths | |
| 0-10 | 1500 | 45 | 6000 | 150 |
| 10-25 | 5000 | 30 | 6000 | 40 |
| 25 - 45 | 3000 | 15 | 5000 | 20 |
| 45 & above | 500 | 22 | 3000 | 54 |
Amit and Rohit started a business by investing ₹20,000 each. After 3 months Amit withdrew ₹5,000 and Rohit put in ₹5,000 additionally. How should a profit of ₹12,800 be divided between them at the end of the year?
A die is thrown 4 times. If ‘getting an odd number’ is a success, find the probability of 2 successes
State whether the following is True or False :
If r.v. X assumes the values 1, 2, 3, ……. 9 with equal probabilities, E(x) = 5.
Solve the following problem :
It is observed that it rains on 10 days out of 30 days. Find the probability that it rains on exactly 3 days of a week.
For the random variable X, if V(X) = 4, E(X) = 3, then E(x2) is ______
Find the mean and variance of the number randomly selected from 1 to 15
A discrete random variable X has the probability distribution given as below:
| X | 0.5 | 1 | 1.5 | 2 |
| P(X) | k | k2 | 2k2 | k |
Determine the mean of the distribution.
The random variable X can take only the values 0, 1, 2. Given that P(X = 0) = P(X = 1) = p and that E(X2) = E[X], find the value of p
The probability distribution of a random variable x is given as under:
P(X = x) = `{{:("k"x^2, "for" x = 1"," 2"," 3),(2"k"x, "for" x = 4"," 5"," 6),(0, "otherwise"):}`
where k is a constant. Calculate E(3X2)
The probability distribution of a random variable x is given as under:
P(X = x) = `{{:("k"x^2, "for" x = 1"," 2"," 3),(2"k"x, "for" x = 4"," 5"," 6),(0, "otherwise"):}`
where k is a constant. Calculate P(X ≥ 4)
The probability distribution of a discrete random variable X is given below:
| X | 2 | 3 | 4 | 5 |
| P(X) | `5/"k"` | `7/"k"` | `9/"k"` | `11/"k"` |
The value of k is ______.
For the following probability distribution:
| X | – 4 | – 3 | – 2 | – 1 | 0 |
| P(X) | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
E(X) is equal to ______.
For the following probability distribution:
| X | 1 | 2 | 3 | 4 |
| P(X) | `1/10` | `3/10` | `3/10` | `2/5` |
E(X2) is equal to ______.
Two numbers are selected from first six even natural numbers at random without replacement. If X denotes the greater of two numbers selected, find the probability distribution of X.
A box contains 30 fruits, out of which 10 are rotten. Two fruits are selected at random one by one without replacement from the box. Find the probability distribution of the number of unspoiled fruits. Also find the mean of the probability distribution.
