Advertisements
Advertisements
Question
Which one of the following is not a function?
Options
(a) {(x, y) : x, y ∈ R, x2 = y}
(b) {(x, y) : x, y ∈, R, y2 = x}
(c) {(x, y) : x, y ∈ R, x2 = y3}
(d) {(x, y) : x, y ∈, R, y = x3}
Solution
(b) {(x, y) : x, y ∈, R, y2 = x}
\[y^2 = x \text{ gives two values of y for a value of x }. \]
\[i . e .\text{ there are two images for a value of x } . \]
\[\text{ For example: } (2 )^2 = 4 \text{ and } ( - 2 )^2 = 4\]
\[\text{ Thus, it is not a function . } \]
APPEARS IN
RELATED QUESTIONS
Find the domain of the function f(x) = `(x^2 + 2x + 1)/(x^2 - 8x + 12)`
Let f be the subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer.
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
If f(x) = x2 − 3x + 4, then find the values of x satisfying the equation f(x) = f(2x + 1).
If \[f\left( x \right) = \frac{2x}{1 + x^2}\] , show that f(tan θ) = sin 2θ.
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] . Then write the value of α satisfying f(f(x)) = x for all x ≠ −1.
If f(x) = 4x − x2, x ∈ R, then write the value of f(a + 1) −f(a − 1).
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
The domain of the function \[f\left( x \right) = \sqrt{\frac{\left( x + 1 \right) \left( x - 3 \right)}{x - 2}}\] is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
The range of the function f(x) = |x − 1| is
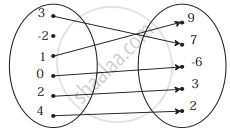
Check if the following relation is function:
If f(m) = m2 − 3m + 1, find `f(1/2)`
If f(m) = m2 − 3m + 1, find f(− x)
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Check if the relation given by the equation represents y as function of x:
2x + 3y = 12
Check if the relation given by the equation represents y as function of x:
x + y2 = 9
If f(m) = m2 − 3m + 1, find f(−3)
If f(m) = m2 − 3m + 1, find f(− x)
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Express the following exponential equation in logarithmic form
e–x = 6
Find the domain of f(x) = ln (x − 5)
Solve for x.
log2 x + log4 x + log16 x = `21/4`
Solve for x.
x + log10 (1 + 2x) = x log10 5 + log10 6
If x = loga bc, y = logb ca, z = logc ab then prove that `1/(1 + x) + 1/(1 + y) + 1/(1 + z)` = 1
Select the correct answer from given alternatives.
If log10(log10(log10x)) = 0 then x =
Select the correct answer from given alternative.
The domain and range of f(x) = 2 − |x − 5| is
Answer the following:
If f(x) = 3x4 – 5x2 + 7 find f(x – 1)
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
Answer the following:
Find the range of the following function.
f(x) = `x/(9 + x^2)`
Given the function f: x → x2 – 5x + 6, evaluate f(– 1)
Given the function f: x → x2 – 5x + 6, evaluate f(2a)
If f(x) = `(x - 1)/(x + 1), x ≠ - 1` Show that f(f(x)) = `- 1/x`, Provided x ≠ 0
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Find the range of the following functions given by f(x) = `3/(2 - x^2)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
If f(x) = x3 – 1 and domain of f = {0, 1, 2, 3}, then domain of f–1 is ______.
