Advertisements
Advertisements
प्रश्न
\[\frac{7x - 5}{8x + 3} > 4\]
उत्तर
We have,
\[\frac{7x - 5}{8x + 3} > 4\]
\[ \Rightarrow \frac{7x - 5}{8x + 3} - 4 > 0\]
\[ \Rightarrow \frac{7x - 5 - 4\left( 8x + 3 \right)}{8x + 3} > 0\]
\[ \Rightarrow \frac{7x - 5 - 32x - 12}{8x + 3} > 0\]
\[ \Rightarrow \frac{- 25x - 17}{8x + 3} > 0\]
\[ \Rightarrow \frac{25x + 17}{8x + 3} < 0 (\text{ Multiplying by - 1 to make the coefficient of x in the LHS hspace{0.167em} positive })\]
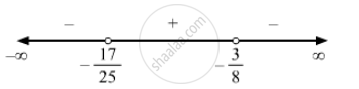
\[x \in \left( \frac{- 17}{25}, \frac{- 3}{8} \right)\]
APPEARS IN
संबंधित प्रश्न
Solve: 12x < 50, when x ∈ R
Solve: 12x < 50, when x ∈ N
Solve: 4x − 2 < 8, when x ∈ R
3x − 7 > x + 1
x + 5 > 4x − 10
\[\frac{3x - 2}{5} \leq \frac{4x - 3}{2}\]
−(x − 3) + 4 < 5 − 2x
\[\frac{x}{5} < \frac{3x - 2}{4} - \frac{5x - 3}{5}\]
\[\frac{6x - 5}{4x + 1} < 0\]
\[\frac{x - 1}{x + 3} > 2\]
Solve each of the following system of equations in R.
2x − 7 > 5 − x, 11 − 5x ≤ 1
2x + 6 ≥ 0, 4x − 7 < 0
Solve each of the following system of equations in R.
3x − 1 ≥ 5, x + 2 > −1
Solve each of the following system of equations in R.
11 − 5x > −4, 4x + 13 ≤ −11
Solve each of the following system of equations in R.
4x − 1 ≤ 0, 3 − 4x < 0
Solve each of the following system of equations in R.
\[\frac{2x - 3}{4} - 2 \geq \frac{4x}{3} - 6, 2\left( 2x + 3 \right) < 6\left( x - 2 \right) + 10\]
Solve each of the following system of equations in R. \[\frac{4}{x + 1} \leq 3 \leq \frac{6}{x + 1}, x > 0\]
Solve
\[\left| \frac{3x - 4}{2} \right| \leq \frac{5}{12}\]
Solve \[\frac{\left| x - 2 \right|}{x - 2} > 0\]
Solve \[\left| x + 1 \right| + \left| x \right| > 3\]
Mark the correct alternative in each of the following:
If − 3x\[+\]17\[< -\]13, then
Mark the correct alternative in each of the following:
Given that x, y and b are real numbers and x\[<\]y, b\[>\]0, then
Mark the correct alternative in each of the following:
If \[\left| x + 3 \right|\]\[\geq\]10, then
Solve 1 ≤ |x – 2| ≤ 3.
Solve for x, |x + 1| + |x| > 3.
Solve the following system of inequalities:
`x/(2x + 1) ≥ 1/4, (6x)/(4x - 1) < 1/2`
If x ≥ –3, then x + 5 ______ 2.
Solve for x, the inequality given below.
`1/(|x| - 3) ≤ 1/2`
Solve for x, the inequality given below.
|x − 1| ≤ 5, |x| ≥ 2
Solve for x, the inequality given below.
`-5 ≤ (2 - 3x)/4 ≤ 9`
If x < 5, then ______.
If |x − 1| > 5, then ______.
If `2/(x + 2) > 0`, then x ______ –2.
If x > – 5, then 4x ______ –20.
If p > 0 and q < 0, then p – q ______ p.
If – 2x + 1 ≥ 9, then x ______ – 4.
