Advertisements
Advertisements
प्रश्न
\[\frac{6x - 5}{4x + 1} < 0\]
उत्तर
\[\frac{6x - 5}{4x + 1} < 0\]
\[\text{ Equating } 6x - 5 \text{ and } 4x + 1 \text{ to zero, we obtain } x = \frac{5}{6} \text{ and } - \frac{1}{4} \text{ as the critical points } . \]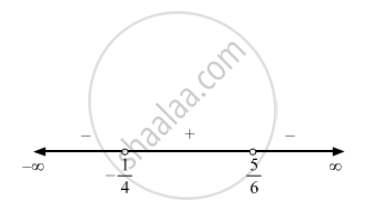
\[\therefore x \in \left( \frac{- 1}{4}, \frac{5}{6} \right)\]
\[\]
APPEARS IN
संबंधित प्रश्न
Solve: 12x < 50, when x ∈ R
Solve: 4x − 2 < 8, when x ∈ N
x + 5 > 4x − 10
3x + 9 ≥ −x + 19
\[\frac{4x + 3}{2x - 5} < 6\]
\[\frac{5x + 8}{4 - x} < 2\]
\[\frac{7x - 5}{8x + 3} > 4\]
Solve each of the following system of equations in R.
x − 2 > 0, 3x < 18
Solve each of the following system of equations in R.
2x + 5 ≤ 0, x − 3 ≤ 0
Solve each of the following system of equations in R.
5x − 1 < 24, 5x + 1 > −24
Solve each of the following system of equations in R.
3x − 1 ≥ 5, x + 2 > −1
Solve each of the following system of equations in R.
4x − 1 ≤ 0, 3 − 4x < 0
Solve each of the following system of equations in R.
\[\frac{2x - 3}{4} - 2 \geq \frac{4x}{3} - 6, 2\left( 2x + 3 \right) < 6\left( x - 2 \right) + 10\]
Solve the following system of equation in R.
\[\frac{2x + 1}{7x - 1} > 5, \frac{x + 7}{x - 8} > 2\]
Solve
\[\left| 4 - x \right| + 1 < 3\]
Solve \[\frac{\left| x - 2 \right|}{x - 2} > 0\]
Solve \[\frac{\left| x + 2 \right| - x}{x} < 2\]
Solve \[\frac{1}{\left| x \right| - 3} \leq \frac{1}{2}\]
Write the solution set of the inequation
\[x + \frac{1}{x} \geq 2\]
Mark the correct alternative in each of the following:
If − 3x\[+\]17\[< -\]13, then
Mark the correct alternative in each of the following:
If x is a real number and \[\left| x \right|\]\[<\]5, then
Mark the correct alternative in each of the following:
\[\left| x - 1 \right|\]\[>\]5, then
Mark the correct alternative in each of the following:
If \[\left| x + 2 \right|\]\[\leq\]9, then
Mark the correct alternative in each of the following:
The inequality representing the following graph is
Mark the correct alternative in each of the following:
The linear inequality representing the solution set given in 
Mark the correct alternative in each of the following:
If \[\left| x + 3 \right|\]\[\geq\]10, then
Solve the inequality, 3x – 5 < x + 7, when x is a whole number.
Solve the inequality, 3x – 5 < x + 7, when x is an integer.
Solve |3 – 4x| ≥ 9.
Solve for x, |x + 1| + |x| > 3.
Solve for x, the inequality given below.
`1/(|x| - 3) ≤ 1/2`
A company manufactures cassettes. Its cost and revenue functions are C(x) = 26,000 + 30x and R(x) = 43x, respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold by the company to realise some profit?
If |x + 2| ≤ 9, then ______.
State which of the following statement is True or False.
If x < –5 and x < –2, then x ∈ (–∞, –5)
If x < –5 and x > 2, then x ∈ (– 5, 2)
If x > y and z < 0, then – xz ______ – yz.
If p > 0 and q < 0, then p – q ______ p.
