Advertisements
Advertisements
प्रश्न
\[\frac{6x - 5}{4x + 1} < 0\]
उत्तर
\[\frac{6x - 5}{4x + 1} < 0\]
\[\text{ Equating } 6x - 5 \text{ and } 4x + 1 \text{ to zero, we obtain } x = \frac{5}{6} \text{ and } - \frac{1}{4} \text{ as the critical points } . \]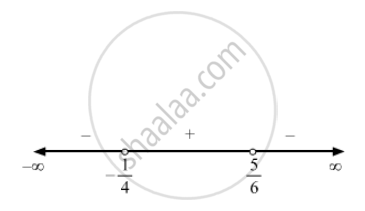
\[\therefore x \in \left( \frac{- 1}{4}, \frac{5}{6} \right)\]
\[\]
APPEARS IN
संबंधित प्रश्न
Solve: 12x < 50, when x ∈ R
Solve: −4x > 30, when x ∈ N
x + 5 > 4x − 10
\[\frac{3x - 2}{5} \leq \frac{4x - 3}{2}\]
−(x − 3) + 4 < 5 − 2x
\[x - 2 \leq \frac{5x + 8}{3}\]
\[\frac{4x + 3}{2x - 5} < 6\]
\[\frac{5x + 8}{4 - x} < 2\]
\[\frac{7x - 5}{8x + 3} > 4\]
Solve each of the following system of equations in R.
\[\frac{7x - 1}{2} < - 3, \frac{3x + 8}{5} + 11 < 0\]
Solve the following system of equation in R.
\[\frac{2x + 1}{7x - 1} > 5, \frac{x + 7}{x - 8} > 2\]
Solve each of the following system of equations in R.
20. −5 < 2x − 3 < 5
Solve each of the following system of equations in R. \[\frac{4}{x + 1} \leq 3 \leq \frac{6}{x + 1}, x > 0\]
Solve
\[\left| 4 - x \right| + 1 < 3\]
Solve \[\left| x - 1 \right| + \left| x - 2 \right| + \left| x - 3 \right| \geq 6\]
Solve \[\left| x + 1 \right| + \left| x \right| > 3\]
Solve \[1 \leq \left| x - 2 \right| \leq 3\]
Mark the correct alternative in each of the following:
If − 3x\[+\]17\[< -\]13, then
Mark the correct alternative in each of the following:
Given that x, y and b are real numbers and x\[<\]y, b\[>\]0, then
Mark the correct alternative in each of the following:
If \[\left| x + 2 \right|\]\[\leq\]9, then
Mark the correct alternative in each of the following:
If \[\left| x + 3 \right|\]\[\geq\]10, then
Solve the inequality, 3x – 5 < x + 7, when x is an integer.
Solve the inequality, 3x – 5 < x + 7, when x is a real number.
Solve `(x - 2)/(x + 5) > 2`.
Solve |3 – 4x| ≥ 9.
The cost and revenue functions of a product are given by C(x) = 20x + 4000 and R(x) = 60x + 2000, respectively, where x is the number of items produced and sold. How many items must be sold to realise some profit?
If x ≥ –3, then x + 5 ______ 2.
If –x ≤ –4, then 2x ______ 8.
Solve for x, the inequality given below.
`-5 ≤ (2 - 3x)/4 ≤ 9`
The water acidity in a pool is considerd normal when the average pH reading of three daily measurements is between 8.2 and 8.5. If the first two pH readings are 8.48 and 8.35, find the range of pH value for the third reading that will result in the acidity level being normal.
In drilling world’s deepest hole it was found that the temperature T in degree celcius, x km below the earth’s surface was given by T = 30 + 25(x – 3), 3 ≤ x ≤ 15. At what depth will the temperature be between 155°C and 205°C?
Given that x, y and b are real numbers and x < y, b < 0, then ______.
If –3x + 17 < –13, then ______.
x and b are real numbers. If b > 0 and |x| > b, then ______.
If |x + 2| ≤ 9, then ______.
If x < –5 and x > 2, then x ∈ (– 5, 2)
If `(-3)/4 x ≤ – 3`, then x ______ 4.
If `2/(x + 2) > 0`, then x ______ –2.
