Advertisements
Advertisements
प्रश्न
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?
उत्तर
Current in the power line, I = 90 A
Point is located below the power line at distance, r = 1.5 m
Hence, magnetic field at that point is given by the relation,
B = `(mu_0 2"I")/(4pi"r")`
Where,
μ0 = Permeability of free space = 4π × 10–7 T m A–1
B = `(4pi xx 10^-7 xx 2 xx 90)/(4pi xx 1.5)`
= 1.2 × 10–5 T
The current is flowing from East to West. The point is below the power line. Hence, according to Maxwell’s right-hand thumb rule, the direction of the magnetic field is towards the South.
APPEARS IN
संबंधित प्रश्न
(a) Write the expression for the magnetic force acting on a charged particle moving with velocity v in the presence of magnetic field B.
Two long, straight, parallel conductors carry steady currents, I1 and I2, separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other? Obtain the expression for this force. Hence, define one ampere.
Seema’s uncle was advised by his doctor to have an MRI (Magnetic Resonance Imaging) scan of his brain. Her uncle felt it to be expensive and wanted to postpone it. When Seema learnt about this, she took the help of her family and also approached the doctor, who also offered a substantial discount. She then convinced her uncle to undergo the test to enable the doctor to know the condition of his brain. The information thus obtained greatly helped the doctor to treat him properly.
Based on the above paragraph, answer the following questions:
(a) What according to you are the values displayed by Seema, her family and the doctor?
(b) What could be the possible reason for MRI test to be so expensive?
(c) Assuming that MRI test was performed using a magnetic field of 0.1 T, find the minimum and maximum values of the force that the magnetic field could exert on a proton (charge = 1.6 x 10-19 C) moving with a speed of 104 m/s.
A circular coil carrying a current I has radius R and number of turns N. If all the three, i.e. the current
I, radius R and number of turns N are doubled, then, the magnetic field at its centre becomes:
(a) Double
(b) Half
(c) Four times
(d) One fourth
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
Write the expression for the Lorentz force F in vector form.
Choose the correct alternative and rewrite the following:
What will happen to the current passing through a resistance, if the potential difference across it is doubled and the resistance is halved?
The force between two parallel current-carrying conductors is F. If the current in each conductor is doubled, then the force between them becomes ______
Explain "Magnetic force never does any work on moving charges".
A proton enters into a magnetic field of induction 1.732 T, with a velocity of 107 m/s at an angle 60° to the field. The force acting on the proton is e = 1.6 × 10-19 C, sin 60° = cos 30° = `sqrt3/2`
A magnetic field set up using Helmholtz coils is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0 × 10–5 V m–1, make a simple guess as to what the beam contains. Why is the answer not unique?
Correct unit of magnetic field is ______.
What is the magnetic induction of the field at the point O in a current I carrying wire that has the shape shown in the figure? The radius of the curved part of the wire is R, the linear parts are assumed to be very long.

In the product
`overset(->)("F") = "q"(overset(->)(υ) xx overset(->)("B"))`
= `"q"overset(->)(υ) xx ("B"overset(^)("i") + "B" overset(^)("j") + "B"_0overset(^)("k"))`
For q = 1 and `overset(->)(υ) = 2overset(^)("i") + 4overset(^)("j") + 6overset(^)("k")` and
`overset(->)("F") = 4overset(^)("i") - 20overset(^)("j") + 12overset(^)("k")`
What will be the complete expression for `overset(->)("B")`?
A circular current loop of magnetic moment M is in an arbitrary orientation in an external magnetic field B. The work done to rotate the loop by 30° about an axis perpendicular to its plane is ______.
At a certain place the angle of dip is 30° and the horizontal component of earth’s magnetic field is 0.5 G. The earth’s total magnetic field (in G), at that certain place, is ______.
A unit vector is represented as `(0.8hat"i" + "b"hat"j" + 0.4hat"k")`. Hence the value of 'b' must be ______.
A long straight conductor kept along X' X axis, carries a steady current I along the +x direction. At an instant t, a particle of mass m and charge q at point (x, y) moves with a velocity `vecv` along +y direction. Find the magnitude and direction of the force on the particle due to the conductor.
Two long parallel current-carrying conductors are 0.4 m apart in air and carry currents 5 A and 10 A. Calculate the force per metre on each conductor, if the currents are (a) in the same direction and (b) in the opposite direction.
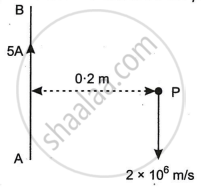
A long straight wire AB carries a current of 5A. P is a proton travelling with a velocity of 2 × 106 m/s, parallel to the wire, 0.2 m from it and in a direction opposite to the current, as shown in Figure below. Calculate the force which magnetic field of the current carrying conductor AB exerts on the proton.