Question

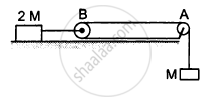
Consider the situation shown in the following figure. Both the pulleys and the string are light and all the surfaces are frictionless.

1. Find the acceleration of the mass M.
2. Find the tension in the string.
3. Calculate the force exerted by the clamp on the pulley A in the figure.

Answer 1

Let the acceleration of mass M be a.
So, the acceleration of mass 2M will be \[\frac{a}{2}\]

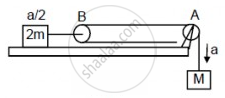
(a)

 

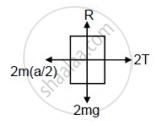
2M(a/2) − 2T = 0
⇒ Ma = 2T
T + Ma − Mg = 0
\[\Rightarrow \frac{Ma}{2} + Ma = Mg \]
\[ \Rightarrow 3Ma = 2Mg\]
\[ \Rightarrow a = \frac{2g}{3}\]

(b) Tension,

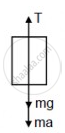
\[T = \frac{Ma}{2} = \frac{M}{2} \times \frac{2g}{3} = \frac{Mg}{3}\] 

(c)

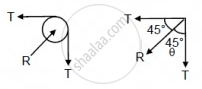
Let T' = resultant of tensions

\[\therefore T' = \sqrt{T^2 + T^2} = \sqrt{2}T\]

\[ \therefore T' = \sqrt{2}T = \frac{\sqrt{2}Mg}{3}\]

\[\text{Again, }\tan\theta = \frac{T}{T} = 1\]

\[ \Rightarrow \theta = 45^\circ\]

So, it is `(sqrt2"Mg")/3` at an angle of 45° with the horizontal.

That is the force exerted by the clamp.