Advertisements
Advertisements
प्रश्न
\[\frac{dy}{dx} = \sin^3 x \cos^2 x + x e^x\]
उत्तर
We have,
\[\frac{dy}{dx} = \sin^3 x \cos^2 x + x e^x \]
\[ \Rightarrow dy = \left( \sin^3 x \cos^2 x + x e^x \right)dx\]
Integrating both sides, we get
\[\int dy = \int\left( \sin^3 x \cos^2 x + x e^x \right)dx\]
\[ \Rightarrow y = \int \sin^3 x \cos^2 x dx + \int x e^x dx \]
\[ \Rightarrow y = I_1 + I_2 . . . . . \left( 1 \right) \]
Here,
\[ I_1 = \int \sin^3 x \cos^2 x dx\]
\[ I_2 = \int x e^x dx\]
Now,
\[ I_1 = \int \sin^3 x \cos^2 x dx\]
\[ = \int\left( 1 - \cos^2 x \right) \cos^2 x \sin x dx\]
\[\text{Putting }t = \cos x,\text{ we get}\]
\[dt = - \sin x dx\]
\[ \therefore I_1 = - \int t^2 \left( 1 - t^2 \right)dt\]
\[ = \int - t^2 + t^4 dt\]
\[ = - \frac{t^3}{3} + \frac{t^5}{5} + C_1 \]
\[ = \frac{\cos^5 x}{5} - \frac{\cos^3 x}{3} + C_1 \]
\[ I_2 = \int x e^x dx\]
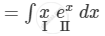
\[ = x\int e^x dx - \int\left( \frac{d}{dx}\left( x \right)\int e^x dx \right)dx\]
\[ = x e^x - e^x + C_2 \]
\[ = \left( x - 1 \right) e^x + C_2 \]
\[\text{Putting the value of }I_1\text{ and }I_2\text{ in (1), we get}\]
\[y = \frac{\cos^5 x}{5} - \frac{\cos^3 x}{3} + C_1 + \left( x - 1 \right) e^x + C_2 \]
\[y = \frac{\cos^5 x}{5} - \frac{\cos^3 x}{3} + \left( x - 1 \right) e^x + C,\text{ where }C = C_1 + C_2\]
APPEARS IN
संबंधित प्रश्न
Write the integrating factor of the following differential equation:
(1+y2) dx−(tan−1 y−x) dy=0
Find the differential equation of the family of lines passing through the origin.
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
y2 = a (b2 – x2)
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
y = e2x (a + bx)
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
y = ex (a cos x + b sin x)
Find the particular solution of the differential equation (1 + e2x) dy + (1 + y2) ex dx = 0, given that y = 1 when x = 0.
Solve the differential equation `ye^(x/y) dx = (xe^(x/y) + y^2)dy, (y != 0)`
Find a particular solution of the differential equation (x - y) (dx + dy) = dx - dy, given that y = -1, when x = 0. (Hint: put x - y = t)
The general solution of the differential equation `(y dx - x dy)/y = 0` is ______.
Find the differential equation of all the circles which pass through the origin and whose centres lie on y-axis.
Find the differential equation of all the circles which pass through the origin and whose centres lie on x-axis.
Form the differential equation having \[y = \left( \sin^{- 1} x \right)^2 + A \cos^{- 1} x + B\], where A and B are arbitrary constants, as its general solution.
The equation of the curve satisfying the differential equation y (x + y3) dx = x (y3 − x) dy and passing through the point (1, 1) is
Verify that xy = a ex + b e−x + x2 is a solution of the differential equation \[x\frac{d^2 y}{d x^2} + 2\frac{dy}{dx} - xy + x^2 - 2 = 0.\]
Show that y2 − x2 − xy = a is a solution of the differential equation \[\left( x - 2y \right)\frac{dy}{dx} + 2x + y = 0.\]
Verify that y = A cos x + sin x satisfies the differential equation \[\cos x\frac{dy}{dx} + \left( \sin x \right)y=1.\]
From x2 + y2 + 2ax + 2by + c = 0, derive a differential equation not containing a, b and c.
\[\frac{dy}{dx} = \frac{1}{x^2 + 4x + 5}\]
\[\frac{dy}{dx} = y^2 + 2y + 2\]
(1 + x) y dx + (1 + y) x dy = 0
Find the general solution of the differential equation `"dy"/"dx" = y/x`.
A solution of the differential equation `("dy"/"dx")^2 - x "dy"/"dx" + y` = 0 is ______.
Find the general solution of the following differential equation:
`x (dy)/(dx) = y - xsin(y/x)`
The general solution of the differential equation `(dy)/(dx) + x/y` = 0 is
If n is any integer, then the general solution of the equation `cos x - sin x = 1/sqrt(2)` is
Solution of the equation 3 tan(θ – 15) = tan(θ + 15) is
The general solution of the differential equation of the type `(dx)/(dy) + p_1y = theta_1` is
Find the general solution of differential equation `(dy)/(dx) = (1 - cosx)/(1 + cosx)`
What is the general solution of differential equation `(dy)/(dx) = sqrt(4 - y^2) (-2 < y < 2)`
The general solution of the differential equation y dx – x dy = 0 is ______.
