Advertisements
Advertisements
प्रश्न
Explain, on the basis of the kinetic theory of gases, how the pressure of a gas changes if its volume is reduced at a constant temperature.
उत्तर १
- At constant temperature, a gas's average kinetic energy per molecule remains constant.
- When a gas's volume is lowered at a constant temperature, the number of gas molecules colliding with the container's walls per unit time increases.
- The momentum transferred per unit time per unit area, i.e. the force exerted by the gas on the walls, increases as a result.
- As a result, the gas pressure rises.
उत्तर २
Let P - be the pressure exerted by the gas
V - be the volume of the gas
N - be the number of molecule of gas
m - be the mass of each molecule of gas.
∴ Total mass of the gas, M = Nm.
From kinetic theory of gases,
`P = (1/3) (Nm)/V barv^2`
∴ Pressure exerted by gas in an enclosed vessel is
`P = 2/3 N/V (1/2mbarv^2)`
But `1/2mbarv^2` = (Kinetic energy at constant temperature)
N is number which is also constant.
∴ `P = "Constant"/V`
∴ `P ∝ 1/V`
As a result, at constant temperature, increasing the pressure of the gas reduces its volume.
APPEARS IN
संबंधित प्रश्न
It is said that the assumptions of kinetic theory are good for gases having low densities. Suppose a container is so evacuated that only one molecule is left in it. Which of the assumptions of kinetic theory will not be valid for such a situation? Can we assign a temperature to this gas?
If the molecules were not allowed to collide among themselves, would you expect more evaporation or less evaporation?
Which of the following parameters is the same for molecules of all gases at a given temperature?
The pressure of an ideal gas is written as \[P = \frac{2E}{3V}\] . Here E refers to
The process on an ideal gas, shown in figure, is
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
The temperature and pressure at Simla are 15.0°C and 72.0 cm of mercury and at Kalka these are 35.0°C and 76.0 cm of mercury. Find the ratio of air density at Kalka to the air density at Simla.
Use R=8.314J K-1 mol-1
The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
Use R = 8.314 JK-1 mol-1
At what temperature the mean speed of the molecules of hydrogen gas equals the escape speed from the earth?
Use R = 8.314 JK-1 mol-1
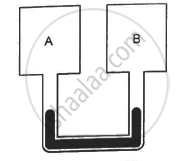
Figure shows two vessels A and B with rigid walls containing ideal gases. The pressure, temperature and the volume are pA, TA, V in the vessel A and pB, TB, V in the vessel B. The vessels are now connected through a small tube. Show that the pressure p and the temperature T satisfy `Ρ/T = 1/2 ({P_A}/{T_A}+{P_B}/{T_B))` when equilibrium is achieved.

An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
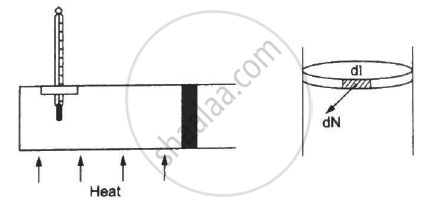
Figure shows a cylindrical tube of radius 5 cm and length 20 cm. It is closed by a tight-fitting cork. The friction coefficient between the cork and the tube is 0.20. The tube contains an ideal gas at a pressure of 1 atm and a temperature of 300 K. The tube is slowly heated and it is found that the cork pops out when the temperature reaches 600 K. Let dN denote the magnitude of the normal contact force exerted by a small length dlof the cork along the periphery (see the figure). Assuming that the temperature of the gas is uniform at any instant, calculate `(dN)/(dt)`.
The temperature and the dew point in an open room are 20°C and 10°C. If the room temperature drops to 15°C, what will be the new dew point?
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
Answer in brief:
Compare the rms speed of hydrogen molecules at 127ºC with rms speed of oxygen molecules at 27ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively.
Two vessels A and B are filled with the same gas where the volume, temperature, and pressure in vessel A is twice the volume, temperature, and pressure in vessel B. Calculate the ratio of the number of molecules of the gas in vessel A to that in vessel B.
Energy is emitted from a hole in an electric furnace at the rate of 20 W when the temperature of the furnace is 727°C. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10-8 Js-1 m-2K-4.)
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (Take Wien's constant b = 2.897 × 10−3 m K)
Find the temperature of a blackbody if its spectrum has a peak at (a) λmax = 700 nm (visible), (b) λmax = 3 cm (microwave region) (c) λmax = 3 m (short radio waves). (Take Wien’s constant b = 2.897 × 10-3 m.K).
The power radiated by a perfect blackbody depends only on its ______
If the density of nitrogen is 1.25 kg/m3 at a pressure of 105 Pa, find the root mean square velocity of nitrogen molecules.
Compare the rate of radiation of metal bodies at 727 °C and 227 °C.
The average K.E. of hydrogen molecules at 27° C is E. The average K.E. at 627° C is ____________.
For a particle moving in vertical circle, the total energy at different positions along the path ______.
When a particle oscillates simple harmonically, its kinetic energy varies periodically. If frequency of the particle is n, then the frequency of the kinetic energy is ______.
According to the kinetic theory of gases, at a given temperature, molecules of all gases have the same ______.
Show that the average energy per molecule is proportional to the absolute temperature T of the gas.
