Advertisements
Advertisements
प्रश्न
Find fog and gof if : f (x) = ex g(x) = loge x .
उत्तर
f (x)=ex, g(x) = loge x
f : R → ( 0, ∞); g : ( 0, ∞) → R
Computing fog:
Clearly, the range of g is a subset of the domain of f.
fog : ( 0, ∞) → R
(fog) (x) = f (g (x))
= f (loge x)
= loge ex
= x
Computing gof:
Clearly, the range of f is a subset of the domain of g .
⇒ fog : R→ R
(gof) (x) = g (f (x))\
= g (ex)
= loge ex
= x
APPEARS IN
संबंधित प्रश्न
Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.
(Hint: Consider f(x) = x + 1 and `g(x) = {(x-1, ifx >1),(1, if x = 1):}`
Let A = {−1, 0, 1} and f = {(x, x2) : x ∈ A}. Show that f : A → A is neither one-one nor onto.
Classify the following function as injection, surjection or bijection :
f : Z → Z, defined by f(x) = x2 + x
Classify the following function as injection, surjection or bijection :
f : Q → Q, defined by f(x) = x3 + 1
Let A = [-1, 1]. Then, discuss whether the following function from A to itself is one-one, onto or bijective : g(x) = |x|
Show that the exponential function f : R → R, given by f(x) = ex, is one-one but not onto. What happens if the co-domain is replaced by`R0^+` (set of all positive real numbers)?
Show that the logarithmic function f : R0+ → R given by f (x) loga x ,a> 0 is a bijection.
Verify associativity for the following three mappings : f : N → Z0 (the set of non-zero integers), g : Z0 → Q and h : Q → R given by f(x) = 2x, g(x) = 1/x and h(x) = ex.
Consider f : N → N, g : N → N and h : N → R defined as f(x) = 2x, g(y) = 3y + 4 and h(z) = sin z for all x, y, z ∈ N. Show that ho (gof) = (hog) of.
Find fog and gof if : f (x) = |x|, g (x) = sin x .
Find fog and gof if : f(x) = c, c ∈ R, g(x) = sin `x^2`
Let f be any real function and let g be a function given by g(x) = 2x. Prove that gof = f + f.
A function f : R → R is defined as f(x) = x3 + 4. Is it a bijection or not? In case it is a bijection, find f−1 (3).
Let f : [−1, ∞) → [−1, ∞) be given by f(x) = (x + 1)2 − 1, x ≥ −1. Show that f is invertible. Also, find the set S = {x : f(x) = f−1 (x)}.
Let f be a function from C (set of all complex numbers) to itself given by f(x) = x3. Write f−1 (−1).
If f : C → C is defined by f(x) = (x − 2)3, write f−1 (−1).
Let f : R → R+ be defined by f(x) = ax, a > 0 and a ≠ 1. Write f−1 (x).
Let f : R → R be defined as `f (x) = (2x - 3)/4.` write fo f-1 (1) .
If f : {5, 6} → {2, 3} and g : {2, 3} → {5, 6} are given by f = {(5, 2), (6, 3)} and g = {(2, 5), (3, 6)}, then find fog. [NCERT EXEMPLAR]
The function
f : A → B defined by
f (x) = - x2 + 6x - 8 is a bijection if
Let
\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = B\] Then, the mapping\[f : A \to \text{B given by} f\left( x \right) = x\left| x \right|\] is
If the function
\[f : R \to R\] be such that
\[f\left( x \right) = x - \left[ x \right]\] where [x] denotes the greatest integer less than or equal to x, then \[f^{- 1} \left( x \right)\]
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] Then, for what value of α is \[f \left( f\left( x \right) \right) = x?\]
A function f: R→ R defined by f(x) = `(3x) /5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f−1.
Consider the set A containing n elements. Then, the total number of injective functions from A onto itself is ______
For sets A, B and C, let f: A → B, g: B → C be functions such that g o f is injective. Then both f and g are injective functions.
For sets A, B and C, let f: A → B, g: B → C be functions such that g o f is surjective. Then g is surjective.
If f: R → R is defined by f(x) = x2 – 3x + 2, write f(f (x))
Let A = {1, 2, 3, ...n} and B = {a, b}. Then the number of surjections from A into B is ______.
If f(x) = (4 – (x – 7)3}, then f–1(x) = ______.
Let f : R → R, g : R → R be two functions such that f(x) = 2x – 3, g(x) = x3 + 5. The function (fog)-1 (x) is equal to ____________.
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever

Let I be the set of all citizens of India who were eligible to exercise their voting right in the general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(V1, V2) ∶ V1, V2 ∈ I and both use their voting right in the general election - 2019}
- Mr. ’X’ and his wife ‘W’ both exercised their voting right in the general election-2019, Which of the following is true?
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let f: R → R be defined by f(x) = x2 is:
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- Let : N → R be defined by f(x) = x2. Range of the function among the following is ____________.
Let f: R→R be defined as f(x) = 2x – 1 and g: R – {1}→R be defined as g(x) = `(x - 1/2)/(x - 1)`. Then the composition function f (g(x)) is ______.
If f: R→R is a function defined by f(x) = `[x - 1]cos((2x - 1)/2)π`, where [ ] denotes the greatest integer function, then f is ______.
The trigonometric equation tan–1x = 3tan–1 a has solution for ______.
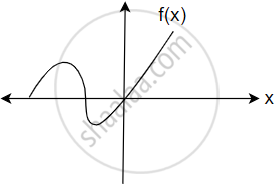
The given function f : R → R is not ‘onto’ function. Give reason.
