Advertisements
Advertisements
प्रश्न
If sin A = `(7)/(25)`, find the value of : `"cos A" + (1)/"cot A"`
उत्तर
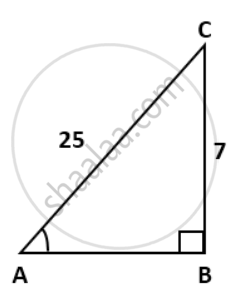
Consider ΔABC, where ∠B = 90°
⇒ sin A = `"Perpendicular"/"Hypotenuse" = "BC"/"AC" = (7)/(25)`
⇒ cosec A = `(1)/"sin A" = (25)/(7)`
By Pythagoras theorem,
AC2 = AB2 + BC2
⇒ AB2
= AC2 - BC2
= 252 - 72
= 625 - 49
= 576
⇒ AB - 24
Now,
cos A = `"Base"/"Hypotenuse" = "AB"/"AC" = (24)/(25)`
tan A = `"Perpendicular"/"Base" = "BC"/"AB" = (7)/(24)`
⇒ cot A = `(1)/"tan A" = (24)/(7)`
`"cos A" + (1)/"cot A"` = cos A + tan A
= `(24)/(25) + (7)/(24)`
= `(576 + 175)/(600)`
= `(751)/(600)`.
APPEARS IN
संबंधित प्रश्न
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of sin A sin B + cos A cos B
If cos θ = `7/25` find the value of all T-ratios of θ .
If sec θ = `5/4 ` show that `((sin θ - 2 cos θ))/(( tan θ - cot θ)) = 12/7`
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
Verify each of the following:
(ii)`cos 60^0 cos 30^0+ sin 60^0 sin30^0`
In the adjoining figure, ΔABC is right-angled at B and ∠A = 450. If AC = 3`sqrt(2)`cm, find (i) BC, (ii) AB.
Form the following figure, find the values of:
- cos B
- tan C
- sin2B + cos2B
- sin B. cos C + cos B. sin C

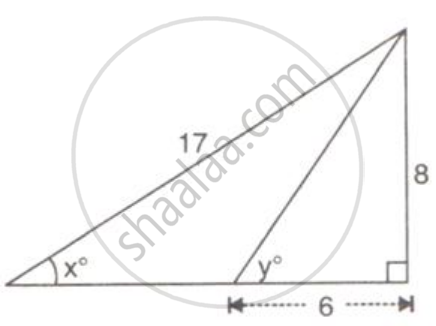
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
From the given figure, find all the trigonometric ratios of angle B
