Advertisements
Advertisements
प्रश्न
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cosec C
उत्तर
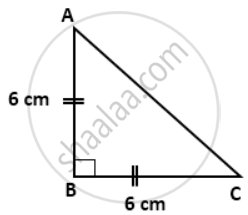
ΔABC is an isosceles right-angled triangle.
∴ AC2
= AB2 + BC2
= 62 + 62
= 36 + 36
= 72
⇒ AC = `6sqrt(2)"cm"`
cosec C
= `"AC"/"AB"`
= `(6sqrt(2))/(6)`
= `sqrt(2)`.
APPEARS IN
संबंधित प्रश्न
In Fig below, Find tan P and cot R. Is tan P = cot R?

f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
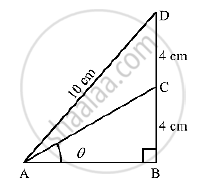
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
If A = 450, verify that :
(i) sin 2A = 2 sin A cos A
If A = 600 and B = 300, verify that:
(ii) cos (A – B) = cos A cos B + sin A sin B
Given: cos A = `( 5 )/ ( 13 )`
Evaluate:
- `(sin "A "–cot "A") / (2 tan "A")`
- `cot "A" + 1/cos"A"`
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
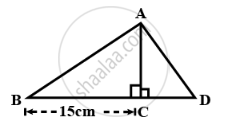
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosB = `(4)/(5)`
If tan = 0.75, find the other trigonometric ratios for A.
