Advertisements
Advertisements
प्रश्न
The value of `cot[cos^-1 (7/25)]` is ______.
विकल्प
`25/24`
`25/7`
`24/25`
`7/24`
उत्तर
The value of `cot[cos^-1 (7/25)]` is `7/24`.
Explanation: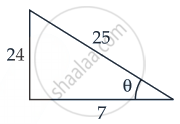
We have, `cot[cos^-1 (7/25)]`
Let `cos^-1 7/25` = θ
∴ cos θ = `7/25`
⇒ cot θ = `7/24`
∴ `cot[cos^-1 (7/25)] = cot[cot^-1 (7/24)] = 7/24`
APPEARS IN
संबंधित प्रश्न
The principal solution of `cos^-1(-1/2)` is :
Write the principal value of `tan^(-1)+cos^(-1)(-1/2)`
The principal solution of the equation cot x=`-sqrt 3 ` is
Solve `3tan^(-1)x + cot^(-1) x = pi`
Find the principal value of the following:
`sin^-1((sqrt3+1)/(2sqrt2))`
Find the principal value of the following:
`sin^-1(cos (3pi)/4)`
For the principal value, evaluate of the following:
`sin^-1(-1/2)+2cos^-1(-sqrt3/2)`
Find the principal value of the following:
`tan^-1(1/sqrt3)`
Find the principal value of the following:
`tan^-1(cos pi/2)`
For the principal value, evaluate of the following:
`tan^-1(-1)+cos^-1(-1/sqrt2)`
Find the principal value of the following:
cosec-1(-2)
Show that `"sin"^-1(5/13) + "cos"^-1(3/5) = "tan"^-1(63/16)`
Solve for x, if:
tan (cos-1x) = `2/sqrt5`
If `sin^-1"x" + tan^-1"x" = pi/2`, prove that `2"x"^2 + 1 = sqrt5`
Prove that tan(cot–1x) = cot(tan–1x). State with reason whether the equality is valid for all values of x.
The value of the expression sin [cot–1 (cos (tan–11))] is ______.
Find the value of `tan^-1 (tan (2pi)/3)`
Find the value of `4tan^-1 1/5 - tan^-1 1/239`
Which of the following is the principal value branch of cos–1x?
Which of the following is the principal value branch of cosec–1x?
If `cos(sin^-1 2/5 + cos^-1x)` = 0, then x is equal to ______.
The value of the expression `2 sec^-1 2 + sin^-1 (1/2)` is ______.
If tan–1x + tan–1y = `(4pi)/5`, then cot–1x + cot–1y equals ______.
The value of `cos^-1 (cos (14pi)/3)` is ______.
If sin `("sin"^-1 1/5 + "cos"^-1 "x") = 1,` then the value of x is ____________.
`"sec" {"tan"^-1 (-"y"/3)}` is equal to ____________.
Which of the following is the principal value branch of `"cos"^-1 "x"`
What is the value of x so that the seven-digit number 8439 × 53 is divisible by 99?
