Advertisements
Advertisements
Question
The value of `cot[cos^-1 (7/25)]` is ______.
Options
`25/24`
`25/7`
`24/25`
`7/24`
Solution
The value of `cot[cos^-1 (7/25)]` is `7/24`.
Explanation: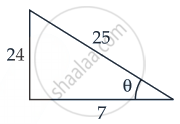
We have, `cot[cos^-1 (7/25)]`
Let `cos^-1 7/25` = θ
∴ cos θ = `7/25`
⇒ cot θ = `7/24`
∴ `cot[cos^-1 (7/25)] = cot[cot^-1 (7/24)] = 7/24`
APPEARS IN
RELATED QUESTIONS
The principal solution of the equation cot x=`-sqrt 3 ` is
For the principal value, evaluate of the following:
`sin^-1(-1/2)+2cos^-1(-sqrt3/2)`
Find the principal value of the following:
`tan^-1(2cos (2pi)/3)`
Find the principal value of the following:
`sec^-1(-sqrt2)`
Find the principal value of the following:
`\text(cosec)^-1(2/sqrt3)`
Find the principal value of the following:
`cot^-1(tan (3pi)/4)`
if sec-1 x = cosec-1 v. show that `1/x^2 + 1/y^2 = 1`
If `sin^-1"x" + tan^-1"x" = pi/2`, prove that `2"x"^2 + 1 = sqrt5`
Find the value of `sin[2cot^-1 ((-5)/12)]`
Find the values of x which satisfy the equation sin–1x + sin–1(1 – x) = cos–1x.
The principal value branch of sec–1 is ______.
If sin–1x + sin–1y = `pi/2`, then value of cos–1x + cos–1y is ______.
Find the value of `tan^-1 (- 1/sqrt(3)) + cot^-1(1/sqrt(3)) + tan^-1(sin((-pi)/2))`
Which of the following is the principal value branch of cos–1x?
The domain of the function cos–1(2x – 1) is ______.
The principal value of `cos^-1 (- 1/2)` is ______.
The value of `sin^-1 (sin (3pi)/5)` is ______.
If `cos(tan^-1x + cot^-1 sqrt(3))` = 0, then value of x is ______.
The value of `cos^-1 (cos (14pi)/3)` is ______.
The value of expression `tan((sin^-1x + cos^-1x)/2)`, when x = `sqrt(3)/2` is ______.
The period of the function f(x) = cos4x + tan3x is ____________.
`"cos" ["tan"^-1 {"sin" ("cot"^-1 "x")}]` is equal to ____________.
If `"tan"^-1 ("a"/"x") + "tan"^-1 ("b"/"x") = pi/2,` then x is equal to ____________.
`"sec" {"tan"^-1 (-"y"/3)}` is equal to ____________.
If `"tan"^-1 "x" + "tan"^-1"y + tan"^-1 "z" = pi/2, "x,y,x" > 0,` then the value of xy+yz+zx is ____________.
Which of the following is the principal value branch of `"cos"^-1 "x"`
What is the principal value of `cot^-1 ((-1)/sqrt(3))`?
Assertion (A): Maximum value of (cos–1 x)2 is π2.
Reason (R): Range of the principal value branch of cos–1 x is `[(-π)/2, π/2]`.
