Advertisements
Online Mock Tests
Chapters
2: Physics and Mathematics
3: Rest and Motion: Kinematics
4: The Forces
5: Newton's Laws of Motion
6: Friction
7: Circular Motion
8: Work and Energy
9: Centre of Mass, Linear Momentum, Collision
10: Rotational Mechanics
11: Gravitation
12: Simple Harmonics Motion
▶ 13: Fluid Mechanics
14: Some Mechanical Properties of Matter
15: Wave Motion and Waves on a String
16: Sound Waves
17: Light Waves
18: Geometrical Optics
19: Optical Instruments
20: Dispersion and Spectra
21: Speed of Light
22: Photometry
![HC Verma solutions for Concepts of Physics Vol. 1 [English] Class 11 and 12 chapter 13 - Fluid Mechanics HC Verma solutions for Concepts of Physics Vol. 1 [English] Class 11 and 12 chapter 13 - Fluid Mechanics - Shaalaa.com](/images/9788177091878-concepts-of-physics-vol-1-english-class-11-and-12_6:46896509a13743528b4d5729ac982f47.jpg)
Advertisements
Solutions for Chapter 13: Fluid Mechanics
Below listed, you can find solutions for Chapter 13 of CBSE, Karnataka Board PUC HC Verma for Concepts of Physics Vol. 1 [English] Class 11 and 12.
HC Verma solutions for Concepts of Physics Vol. 1 [English] Class 11 and 12 13 Fluid Mechanics Short Answers [Pages 270 - 271]
Is it always true that the molecules of a dense liquid are heavier than the molecules of a lighter liquid?
If someone presses a pointed needle against your skin, you are hurt. But if someone presses a rod against your skin with the same force, you easily tolerate. Explain.
In the derivation of P1 − P2 = ρgz, it was assumed that the liquid is incompressible. Why will this equation not be strictly valid for a compressible liquid?
Suppose the density of air at Madras is ρo and atmospheric pressure is P0. If we go up, the density and the pressure both decrease. Suppose we wish to calculate the pressure at a height 10 km above Madras. If we use the equation Po − P = ρogz, will we get a pressure more than the actual or less than the actual? Neglect the variation in g. Does your answer change if you also consider the variation in g?
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
A barometer tube reads 76 cm of mercury. If the tube is gradually inclined keeping the open end immersed in the mercury reservoir, will the length of mercury column be 76 cm, more than 76 cm or less than 76 cm?
A one meter long glass tube is open at both ends. One end of the tube is dipped into a mercury cup, the tube is kept vertical and the air is pumped out of the tube by connecting the upper end to a suction pump. Can mercury be pulled up into the pump by this process?
A satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1 m long placed in the satellite?
Consider the barometer shown in the following figure. If a small hole is made at a point P in the barometer tube, will the mercury come out from this hole?
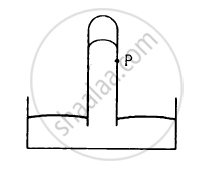
Is Archimedes' principle valid in an elevator accelerating up ? In a car accelerating on a level road?
Why is it easier to swim in sea water than in fresh water?
A glass of water has an ice cube floating in water. The water level just touches the rim of the glass. Will the water overflow when the ice melts?
A ferry boat loaded with rocks has to pass under a bridge. The maximum height of the rocks is slightly more than the height of the bridge so that the boat just fails to pass under the bridge. Should some of the rocks be removed or some more rocks be added?
Water is slowly coming out from a vertical pipe. As the water descends after coming out, its area of cross section reduces. Explain this on the basis of the equation of continuity.
While watering a distant plant, a gardener partially closes the exit hole of the pipe by putting his finger on it. Explain why this results in the water stream going to a larger distance.
A Gipsy car has a canvass top. When the car runs at high speed, the top bulges out. Explain.
HC Verma solutions for Concepts of Physics Vol. 1 [English] Class 11 and 12 13 Fluid Mechanics MCQ [Pages 271 - 272]
A liquid can easily change its shape but a solid can not because
the density of a liquid is smaller than that of a solid
the forces between the molecules is stronger in solid than in liquids
the atoms combine to form bigger molecules in a solid
the average separation between the molecules is larger in solids
Consider the equations `P=lim_(triangles->0)"F"/(triangle"S")` and P1 - P2 = pgz. In an elevator accelerating upward
both the equations are valid
the first is valid but not the second
the second is valid but not the first
both are invalid
The three vessels shown in the following figure have same base area. Equal volumes of a liquid are poured in the three vessels. The force on the base will be
maximum in vessel A
maximum in vessel B
maximum in vessel C
equal in all the vessels
Equal mass of three liquids are kept in three identical cylindrical vessels A, B and C. The densities are ρA, ρB, ρC with ρA < ρB < ρC. The force on the base will be
maximum in vessel A
maximum in vessel B
maximum in vessel C
equal in all the vessels
Shows in the following figure a siphon. The liquid shown is water. The pressure difference PB − PAbetween the points A and B is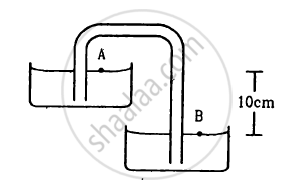
400 Nm−2
3000 Nm−2
1000 Nm−2
1000 Nm−2
Zero
A beaker containing a liquid is kept inside a big closed jar. If the air inside the jar is continuously pumped out, the pressure in the liquid near the bottom of the liquid will
increase
decrease
remain constant
first decrease and then increase
The pressure in a liquid at two points in the same horizontal plane are equal. Consider an elevator accelerating upward and a car accelerating on a horizontal road. The above statement is correct in
the car only
the elevator only
both of them
neither of them
Suppose the pressure at the surface of mercury in a barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
P1 = 0, P2 = atmospheric pressure
P1 = atmospheric pressure P2 = 0
P1 = P2 = atmospheric pressure
P1 = P2 = 0
A barometer kept in an elevator reads 76 cm when it is at rest. If the elevator goes up with increasing speed, the reading will be ______.
zero
76 cm
< 76 cm
> 76 cm
A barometer kept in an elevator accelerating upward reads 76 cm. The air pressure in the elevator is
76 cm
< 76 cm
> 76 cm
zero
To construct a barometer, a tube of length 1 m is filled completely with mercury and is inverted in a mercury cup. The barometer reading on a particular day is 76 cm. Suppose a 1 m tube is filled with mercury up to 76 cm and then closed by a cork. It is inverted in a mercury cup and the cork is removed. The height of mercury column in the tube over the surface in the cup will be
zero
76 cm
> 76 cm
< 76 cm
A 20 N metal block is suspended by a spring balance. A beaker containing some water is placed on a weighing machine which reads 40 N. The spring balance is now lowered so that the block gets immersed in the water. The spring balance now reads 16 N. The reading of the weighing machine will be
36 N
60 N
44 N
56 N
A piece of wood is floating in water kept in a bottle. The bottle is connected to an air pump. Neglect the compressibility of water. When more air is pushed into the bottle from the pump, the piece of wood will float with
larger part in the water
lesser part in the water
same part in the water
it will sink
A metal cube is placed in an empty vessel. When water is filled in the vessel so that the cube is completely immersed in the water, the force on the bottom of the vessel in contact with the cube
will increase
will decrease
will remain the same
will become zero
A wooden object floats in water kept in a beaker. The object is near a side of the beaker . Let P1, P2, P3 be the pressures at the three points A, B and C of bottom as shown in the figure.
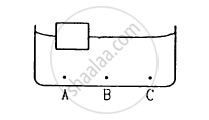
P1 = P2 = P3
P1 < P2 < P3
P1 > P2 > P3
P2 = P3 ≠ P1
A closed cubical box is completely filled with water and is accelerated horizontally towards right with an acceleration α. The resultant normal force by the water on the top of the box
passes through the centre of the top
passes through a point to the right of the centre
passes through a point to the left of the centre
becomes zeros
Consider the situation of the previous problem. Let the water push the left wall by a force F1 and the right wall by a force F2.
F1 = F2
F1 > F2
F1 < F2
the information is insufficient to know the relation between F1 and F2
Water enters through end A with a speed v1 and leaves through end B with a speed v2 of a cylindrical tube AB. The tube is always completely filled with water. In case I the tube is horizontal, in case II it is vertical with the end A upward and in case III it is vertical with the end B upward. We have v1 = v2 for
case I
case II
case III
each case
Bernoulli's theorem is based on the conservation of
Linear momentum
Mass
Energy
Angular momentum
Water is flowing through a long horizontal tube. Let PA and PB be the pressures at two points A and B of the tube.
PA must be equal to PB.
PA must be greater than PB.
PA must be smaller than PB.
PA = PB only if the cross-sectional area at A and B are equal.
Water and mercury are filled in two cylindrical vessels up to same height. Both vessels have a hole in the wall near the bottom. The velocity of water and mercury coming out of the holes are v1 and v2 respectively.
v1 = v2
v1 = 13.6 v2
v1 = v2/13.6
- \[\text{v}_1 = \sqrt{13 . 6} \text{v}_2\]
A large cylindrical tank has a hole of area A at its bottom. Water is poured in the tank by a tube of equal cross-sectional area A ejecting water at the speed v.
The water level in the tank will keep on rising
No water can be stored in the tank
The water level will rise to a height v2/2g and then stop
The water level will oscillate
HC Verma solutions for Concepts of Physics Vol. 1 [English] Class 11 and 12 13 Fluid Mechanics MCQ [Pages 272 - 273]
A solid floats in a liquid in a partially dipped position.
(a) The solid exerts a force equal to its weight on the liquid.
(b) The liquid exerts a force of buoyancy on the solid which is equal to the weight of the solid.
(c) The weight of the displaced liquid equals the weight of the solid.
(d) The weight of the dipped part of the solid is equal to the weight of the displaced liquid.
The weight of an empty balloon on a spring balance is W1. The weight becomes W2when the balloon is filled with air. Let the weight of the air itself be w. Neglect the thickness of the balloon when it is filled with air. Also neglect the difference in the densities of air inside and outside the balloon.
(a) W2 = W1
(b) W2 = W1 + w
(c) W2 < W1 + w
(d) W2 > W1
A solid is completely immersed in a liquid. The force exerted by the liquid on the solid will
(a) increase if it is pushed deeper inside the liquid
(b) change if its orientation is changed
(c) decrease if it is taken partially out of the liquid
(d) be in the vertically upward direction.
A closed vessel is half filled with water. There is a hole near the top of the vessel and air is pumped out from this hole.
(a) The water level will rise up in the vessel.
(b) The pressure at the surface of the water will decrease
(c) The force by the water on the bottom of the vessel will decrease
(d) The density of the liquid will decrease
In a streamline flow,
(a) the speed of a particle always remains same
(b) the velocity of a particle always remains same
(c) the kinetic energies of all the particles arriving at a given point are the same
(d) the momenta of all the particles arriving at a given point are the same
Water flows through two identical tubes A and B. A volume V0 of water passes through the tube A and 2 V0 through B in a given time. Which of the following may be correct?
(a) Flow in both the tubes are steady.
(b) Flow in both the tubes are turbulent.
(c) Flow is steady in A but turbulent in B.
(d) Flow is steady in B but turbulent in A.
Water is flowing in streamline motion through a tube with its axis horizontal. Consider two points A and B in the tube at the same horizontal level.
(a) The pressures at A and B are equal for any shape of the tube.
(b) The pressures are never equal.
(c) The pressures are equal if the tube has a uniform cross section.
(d) The pressures may be equal even if the tube has a nonuniform cross section.
There is a small hole near the bottom of an open tank filled with a liquid. The speed of the water ejected does not depend on
(a) area of the hole
(b) density of the liquid
(c) height of the liquid from the hole
(d) acceleration due to gravity
HC Verma solutions for Concepts of Physics Vol. 1 [English] Class 11 and 12 13 Fluid Mechanics Exercise [Pages 273 - 275]
The surface of water in a water tank on the top of a house is 4 m above the tap level. Find the pressure of water at the tap when the tap is closed. Is it necessary to specify that the tap is closed?
The heights of mercury surfaces in the two arms of the manometer shown in figure are 2 cm and 8 cm.
Atmospheric pressure = 1.01 × 105 N−2. Find (a) the pressure of the gas in the cylinder and (b) the pressure of mercury at the bottom of the U tube.
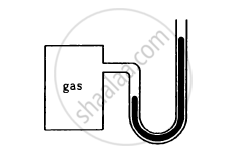
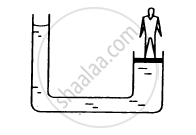
The area of cross section of the wider tube shown in figure is 900 cm2. If the boy standing on the piston weighs 45 kg, find the difference in the levels of water in the two tubes.
A glass full of water has a bottom of area 20 cm2, top of area 20 cm2, height 20 cm and volume half a litre.
(a) Find the force exerted by the water on the bottom.
(b) Considering the equilibrium of the water, find the resultant force exerted by the sides of the glass on the water. Atmospheric pressure = 1.0 × 105 N/m2. Density of water 1000 kg/m3 and g = 10 m/s2. Take all numbers
to be exact.
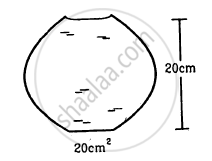
Suppose the glass of the previous problem is covered by a jar and the air inside the jar is completely pumped out. (a) What will be the answers to the problem? (b) Show that the answers do not change if a glass of different shape is used provided the height, the bottom area and the volume are unchanged.
If water be used to construct a barometer, what would be the height of water column at standard atmospheric pressure (76 cm of mercury) ?
Find the force exerted by the water on a 2 m2 plane surface of a large stone placed at the bottom of a sea 500 m deep. Does the force depend on the orientation of the surface?
Water is filled in a rectangular tank of size 3 m × 2 m × 1 m. (a) Find the total force exerted by the water on the bottom surface on the tank. (b) Consider a vertical side of area 2 m × 1 m. Take a horizontal strip of width δx metre in this side, situated at a depth of x metre from the surface of water. Find the force by the water on this strip. (c) Find the torque of the force calculate in part (b) about the bottom edge of this side.
(d) Find the total force by the water on this side.
(e) Find the total torque by the water on the side about the bottom edge. Neglect the atmospheric pressure and take g = 10 ms−2.
An ornament weighing 36 g in air, weighs only 34 g in water. Assuming that some copper is mixed with gold to prepare the ornament, find the amount of copper in it. Specific gravity of gold is 19.3 and that of copper is 8.9.
Refer to the previous problem. Suppose, the goldsmith argues that he has not mixed copper or any other material with gold, rather some cavities might have been left inside the ornament. Calculate the volume of the cavities left that will allow the weights given in that problem.
A metal piece of mass 160 g lies in equilibrium inside a glass of water. The piece touches the bottom of the glass at a small number of points. If the density of the metal is 8000 kg/m3, find the normal force exerted by the bottom of the glass on the metal piece.

A ferry boat has internal volume 1 m3 and weight 50 kg.(a) Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water.(b) If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
A cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. Water can be the minimum edge of the block so that it does not sink in water? Specific gravity of ice = 0.9.
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

A cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron = 8000 kg/m3 and density of water = 1000 kg/m3.
A cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
A hollow spherical body of inner and outer radii 6 cm and 8 cm respectively floats half-submerged in water. Find the density of the material of the sphere.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
Find the ratio of the weights, as measured by a spring balance, of a 1 kg block of iron and a 1 kg block of wood. Density of iron = 7800 kg/m3, density of wood = 800 kg/m3and density of air = 1.293 kg/m3.
A cylindrical object of outer diameter 20 cm and mass 2 kg floats in water with its axis vertical. If it is slightly depressed and then released, find the time period of the resulting simple harmonic motion of the object.
A cylindrical object of outer diameter 10 cm, height 20 cm and density 8000 kg/m3 is supported by a vertical spring and is half dipped in water as shown in figure. (a) Find the elongation of the spring in equilibrium condition. (b) If the object is slightly depressed and released, find the time period of resulting oscillations of the object. The spring constant = 500 N/m.
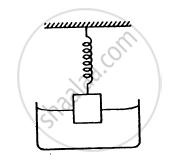
A wooden block of mass 0.5 kg and density 800 kg/m3 is fastened to the free end of a vertical spring of spring constant 50 N/m fixed at the bottom. If the entire system is completely immersed in water, find the elongation (or compression) of the spring in equilibrium .
A wooden block of mass 0.5 kg and density 800 kg/m3 is fastened to the free end of a vertical spring of spring constant 50 N/m1 fixed at the bottom. If the entire system is completely immersed in water, find the time-period of vertical oscillations of the block when it is slightly depressed and released.
A cube of ice of edge 4 cm is placed in an empty cylindrical glass of inner diameter 6 cm. Assume that the ice melts uniformly from each side so that it always retains its cubical shape. Remembering that ice is lighter than water, find the length of the edge of the ice cube at the instant it just leaves contact with the bottom of the glass.
A U-tube containing a liquid is accelerated horizontally with a constant acceleration a0. If the separation between the vertical limbs is l, find the difference in the heights of the liquid in the two arms.
At Deoprayag (Garwal, UP) river Alaknande mixes with the river Bhagirathi and becomes river Ganga. Suppose Alaknanda has a width of 12 m, Bhagirathi has a width of 8 m and Ganga has a width of 16 m. Assume that the depth of water is same in the three rivers, Let the average speed of water in Alaknanda be 20 km/h and in Bhagirathi be 16 km/h. Find the average speed of water in the river Ganga.
Water flows through a horizontal tube of variable cross section. The area of cross section at A and B are 4 mm2 and 2 mm2 respectively. If 1 cc of water enters per second through A, find (a) the speed of water at A, (b) the speed of water at B and (c) the pressure difference PA − PB.

Suppose the tube in the previous problem is kept vertical with A upward but the other conditions remain the same. the separation between the cross sections at A and B is 15/16 cm. Repeat parts (a), (b) and (c) of the previous problem. Take g = 10 m/s2.
Suppose the tube in the previous problem is kept vertical with B upward. Water enters through B at the rate of 1 cm3/s. Repeat parts (a), (b) and (c). Note that the speed decreases as the water falls down.
Water flows through a tube shown in figure. The area of cross section at A and B are 1 cm2 and 0.5 cm2 respectively. The height difference between A and B is 5 cm. If the speed of water at A is 10 cm s find (a) the speed at B and (b) the difference in pressures at A and B.

Water flows through a horizontal tube as shown in figure. If the difference of heights of water column in the vertical tubes is 2 cm, and the areas of cross section at A and B are 4 cm2 and 2 cm2 respectively, find the rate of flow of water across any section.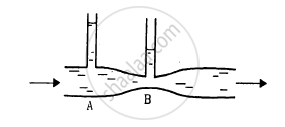
Water flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5 cm2 and 2 cm2 respectively. The rate of flow of water through the tube is 500 cm3 s−1. Find the difference of mercury levels in the U-tube.
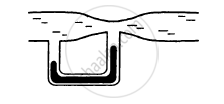
Water leaks out from an open tank through a hole of area 2 mm2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tanks is 0.4 m2. The pressure at the open surface and at the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. (a) Find the initial speed of water coming out of the hole. (b) Find the speed of water coming out when half of water has leaked out. (c) Find the volume of eater leaked out using a time interval dt after the height remained is h. Thus find the decrease in height dh in terms of h and dt.
(d) From the result of park (c) find the time required for half of the water to leak out.
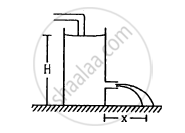
Water level is maintained in a cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
Solutions for 13: Fluid Mechanics
![HC Verma solutions for Concepts of Physics Vol. 1 [English] Class 11 and 12 chapter 13 - Fluid Mechanics HC Verma solutions for Concepts of Physics Vol. 1 [English] Class 11 and 12 chapter 13 - Fluid Mechanics - Shaalaa.com](/images/9788177091878-concepts-of-physics-vol-1-english-class-11-and-12_6:46896509a13743528b4d5729ac982f47.jpg)
HC Verma solutions for Concepts of Physics Vol. 1 [English] Class 11 and 12 chapter 13 - Fluid Mechanics
Shaalaa.com has the CBSE, Karnataka Board PUC Mathematics Concepts of Physics Vol. 1 [English] Class 11 and 12 CBSE, Karnataka Board PUC solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. HC Verma solutions for Mathematics Concepts of Physics Vol. 1 [English] Class 11 and 12 CBSE, Karnataka Board PUC 13 (Fluid Mechanics) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. HC Verma textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Concepts of Physics Vol. 1 [English] Class 11 and 12 chapter 13 Fluid Mechanics are Introduction of Mechanical Properties of Fluids, Archimedes' Principle, Stoke's Law, Equation of Continuity, Torricelli's Law, Variation of Pressure with Depth, Atmospheric Pressure and Gauge Pressure, Hydraulic Machines, Streamline and Turbulent Flow, Applications of Bernoulli’s Equation, Reynold's Number, Effect of Gravity on Fluid Pressure, Terminal Velocity, Critical Velocity, Excess of Pressure Across a Curved Surface, Thrust and Pressure, Pascal’s Law, Surface Tension, Viscous Force or Viscosity.
Using HC Verma Concepts of Physics Vol. 1 [English] Class 11 and 12 solutions Fluid Mechanics exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in HC Verma Solutions are essential questions that can be asked in the final exam. Maximum CBSE, Karnataka Board PUC Concepts of Physics Vol. 1 [English] Class 11 and 12 students prefer HC Verma Textbook Solutions to score more in exams.
Get the free view of Chapter 13, Fluid Mechanics Concepts of Physics Vol. 1 [English] Class 11 and 12 additional questions for Mathematics Concepts of Physics Vol. 1 [English] Class 11 and 12 CBSE, Karnataka Board PUC, and you can use Shaalaa.com to keep it handy for your exam preparation.
