Question

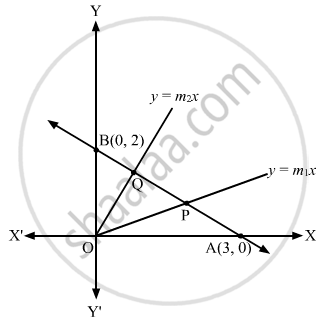
Find the equations of the straight lines which pass through the origin and trisect the portion of the straight line 2x + 3y = 6 which is intercepted between the axes.

Answer 1

Let the line 2x + 3y = 6 intersect the x-axis and the y-axis at A and B, respectively.
At x = 0 we have,
0 + 3y = 6

\[\Rightarrow\] y = 2
At y = 0 we have,
2x + 0 = 6

\[\Rightarrow\] x = 3

\[\therefore A \equiv \left( 3, 0 \right) \text { and } B \equiv \left( 0, 2 \right)\]

Let \[y = m_1 x \text { and } y = m_2 x\] pass through the origin trisecting the line 2x + 3y = 6 at P and Q.
∴ AP = PQ = QB

Let us find the coordinates of P and Q using the section formula.

\[P \equiv \left( \frac{2 \times 3 + 1 \times 0}{2 + 1}, \frac{2 \times 0 + 1 \times 2}{2 + 1} \right) = \left( 2, \frac{2}{3} \right)\]

\[Q \equiv \left( \frac{1 \times 3 + 2 \times 0}{2 + 1}, \frac{1 \times 0 + 2 \times 2}{2 + 1} \right) = \left( 1, \frac{4}{3} \right)\]

Clearly, P and Q lie on \[y = m_1 x \text { and } y = m_2 x\],  respectively.

\[\therefore \frac{2}{3} = m_1 \times 2 \text { and } \frac{4}{3} = m_2 \times 1\]

\[ \Rightarrow m_1 = \frac{1}{3} \text { and } m_2 = \frac{4}{3}\]

Hence, the required lines are

\[y = \frac{1}{3}x \text { and } y = \frac{4}{3}x\]

⇒ x − 3y = 0 and 4x − 3y = 0