Advertisements
Advertisements
प्रश्न
Find the slope of the tangent to the curve y = 3x4 − 4x at x = 4.
उत्तर
The given curve is y = 3x4 − 4x.
Then, the slope of the tangent to the given curve at x = 4 is given by,
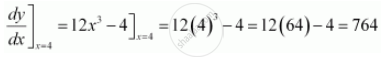
APPEARS IN
संबंधित प्रश्न
Find the equation of the normal at a point on the curve x2 = 4y which passes through the point (1, 2). Also find the equation of the corresponding tangent.
Find the equation of all lines having slope 2 which are tangents to the curve `y = 1/(x- 3), x != 3`
Find the equations of the tangent and normal to the given curves at the indicated points:
y = x4 − 6x3 + 13x2 − 10x + 5 at (1, 3)
Find the equations of the tangent and normal to the given curves at the indicated points:
y = x3 at (1, 1)
Find the equation of the normal at the point (am2, am3) for the curve ay2 = x3.
Find the points on the curve y = `4x^3 - 3x + 5` at which the equation of the tangent is parallel to the x-axis.
Find the slope of the tangent and the normal to the following curve at the indicted point x = a (θ − sin θ), y = a(1 − cos θ) at θ = π/2 ?
Find the slope of the tangent and the normal to the following curve at the indicted point y = (sin 2x + cot x + 2)2 at x = π/2 ?
Find the points on the curve xy + 4 = 0 at which the tangents are inclined at an angle of 45° with the x-axis ?
Find the points on the curve y = 3x2 − 9x + 8 at which the tangents are equally inclined with the axes ?
At what points on the curve y = 2x2 − x + 1 is the tangent parallel to the line y = 3x + 4?
Find the equation of the tangent and the normal to the following curve at the indicated point y = x2 at (0, 0) ?
Find the equation of the tangent and the normal to the following curve at the indicated point \[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \text { at } \left( a\sec\theta, b\tan\theta \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point 4x2 + 9y2 = 36 at (3cosθ, 2sinθ) ?
Find the equation of the tangent and the normal to the following curve at the indicated points \[x = \frac{2 a t^2}{1 + t^2}, y = \frac{2 a t^3}{1 + t^2}\text { at } t = \frac{1}{2}\] ?
Find the equation of the tangent and the normal to the following curve at the indicated points x = at2, y = 2at at t = 1 ?
Find the equation of the tangent and the normal to the following curve at the indicated points x = a(θ + sinθ), y = a(1 − cosθ) at θ ?
Find the equation of the tangent to the curve x2 + 3y − 3 = 0, which is parallel to the line y= 4x − 5 ?
Find the angle of intersection of the following curve x2 + y2 = 2x and y2 = x ?
Show that the following set of curve intersect orthogonally y = x3 and 6y = 7 − x2 ?
Show that the following set of curve intersect orthogonally x3 − 3xy2 = −2 and 3x2y − y3 = 2 ?
Find the point on the curve y = x2 − 2x + 3, where the tangent is parallel to x-axis ?
Find the slope of the tangent to the curve x = t2 + 3t − 8, y = 2t2 − 2t − 5 at t = 2 ?
Write the angle between the curves y2 = 4x and x2 = 2y − 3 at the point (1, 2) ?
Write the coordinates of the point at which the tangent to the curve y = 2x2 − x + 1 is parallel to the line y = 3x + 9 ?
At what point the slope of the tangent to the curve x2 + y2 − 2x − 3 = 0 is zero
Find the angle of intersection of the curves y2 = 4ax and x2 = 4by.
The tangent to the curve given by x = et . cost, y = et . sint at t = `pi/4` makes with x-axis an angle ______.
The equation of the normal to the curve y = sinx at (0, 0) is ______.
Find the angle of intersection of the curves y = 4 – x2 and y = x2.
The equation of normal to the curve y = tanx at (0, 0) is ______.
The points on the curve `"x"^2/9 + "y"^2/16` = 1 at which the tangents are parallel to the y-axis are:
The two curves x3 - 3xy2 + 5 = 0 and 3x2y - y3 - 7 = 0
The tangent to the curve y = x2 + 3x will pass through the point (0, -9) if it is drawn at the point ____________.
Find the equation of the tangent line to the curve y = x2 − 2x + 7 which is parallel to the line 2x − y + 9 = 0.
Tangent and normal are drawn at P(16, 16) on the parabola y2 = 16x, which intersect the axis of the parabola at A and B, respectively. If C is the centre of the circle through the points P, A and B and ∠CPB = θ, then a value of tan θ is:
Let `y = f(x)` be the equation of the curve, then equation of normal is
