Advertisements
Advertisements
Question
Find the slope of the tangent to the curve y = 3x4 − 4x at x = 4.
Solution
The given curve is y = 3x4 − 4x.
Then, the slope of the tangent to the given curve at x = 4 is given by,
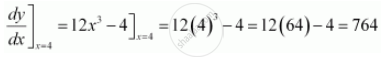
APPEARS IN
RELATED QUESTIONS
The equation of tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x – 5. Find the values of a and b.
Find a point on the curve y = (x − 2)2 at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
Find the equations of the tangent and normal to the given curves at the indicated points:
y = x4 − 6x3 + 13x2 − 10x + 5 at (1, 3)
Find the equations of the tangent and normal to the given curves at the indicated points:
y = x3 at (1, 1)
Find the equations of the tangent and normal to the given curves at the indicated points:
x = cos t, y = sin t at t = `pi/4`
Find the slope of the tangent and the normal to the following curve at the indicted point x = a (θ − sin θ), y = a(1 − cos θ) at θ = π/2 ?
Find the values of a and b if the slope of the tangent to the curve xy + ax + by = 2 at (1, 1) is 2 ?
Find the point on the curve y = x2 where the slope of the tangent is equal to the x-coordinate of the point ?
At what points on the circle x2 + y2 − 2x − 4y + 1 = 0, the tangent is parallel to x-axis?
Find the points on the curve y = 3x2 − 9x + 8 at which the tangents are equally inclined with the axes ?
Find the point on the curve y = 3x2 + 4 at which the tangent is perpendicular to the line whose slop is \[- \frac{1}{6}\] ?
Find the points on the curve x2 + y2 = 13, the tangent at each one of which is parallel to the line 2x + 3y = 7 ?
Find the equation of the tangent and the normal to the following curve at the indicated point \[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \text { at } \left( a\sec\theta, b\tan\theta \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point y2 = 4ax at \[\left( \frac{a}{m^2}, \frac{2a}{m} \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point \[x^\frac{2}{3} + y^\frac{2}{3}\] = 2 at (1, 1) ?
Find the equation of the tangent and the normal to the following curve at the indicated point y2 = 4x at (1, 2) ?
Find the equation of the tangent and the normal to the following curve at the indicated point 4x2 + 9y2 = 36 at (3cosθ, 2sinθ) ?
The equation of the tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x − 5. Find the values of a and b ?
Prove that \[\left( \frac{x}{a} \right)^n + \left( \frac{y}{b} \right)^n = 2\] touches the straight line \[\frac{x}{a} + \frac{y}{b} = 2\] for all n ∈ N, at the point (a, b) ?
Find the angle of intersection of the following curve 2y2 = x3 and y2 = 32x ?
Find the angle of intersection of the following curve x2 + 4y2 = 8 and x2 − 2y2 = 2 ?
Find the condition for the following set of curve to intersect orthogonally \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \text { and } \frac{x^2}{A^2} - \frac{y^2}{B^2} = 1\] ?
Show that the curves \[\frac{x^2}{a^2 + \lambda_1} + \frac{y^2}{b^2 + \lambda_1} = 1 \text { and } \frac{x^2}{a^2 + \lambda_2} + \frac{y^2}{b^2 + \lambda_2} = 1\] intersect at right angles ?
Write the coordinates of the point on the curve y2 = x where the tangent line makes an angle \[\frac{\pi}{4}\] with x-axis ?
Write the angle made by the tangent to the curve x = et cos t, y = et sin t at \[t = \frac{\pi}{4}\] with the x-axis ?
Write the slope of the normal to the curve \[y = \frac{1}{x}\] at the point \[\left( 3, \frac{1}{3} \right)\] ?
Write the equation of the tangent drawn to the curve \[y = \sin x\] at the point (0,0) ?
The equation of the normal to the curve y = x + sin x cos x at x = `π/2` is ___________ .
The point on the curve y2 = x where tangent makes 45° angle with x-axis is ____________________ .
The equation of the normal to the curve x = a cos3 θ, y = a sin3 θ at the point θ = π/4 is __________ .
The angle of intersection of the curves y = 2 sin2 x and y = cos 2 x at \[x = \frac{\pi}{6}\] is ____________ .
Find the condition for the curves `x^2/"a"^2 - y^2/"b"^2` = 1; xy = c2 to interest orthogonally.
The abscissa of the point on the curve 3y = 6x – 5x3, the normal at which passes through origin is ______.
The tangent to the curve y = e2x at the point (0, 1) meets x-axis at ______.
If `tan^-1x + tan^-1y + tan^-1z = pi/2`, then
The Slope of the normal to the curve `y = 2x^2 + 3 sin x` at `x` = 0 is
An edge of variable cube is increasing at the rate of 3 cm/s. The volume of the cube increasing fast when the edge is 10 cm long is ______ cm3/s.
If the tangent to the conic, y – 6 = x2 at (2, 10) touches the circle, x2 + y2 + 8x – 2y = k (for some fixed k) at a point (α, β); then (α, β) is ______.
