Advertisements
Advertisements
प्रश्न
Find the slope of the tangent to the curve y = 3x4 − 4x at x = 4.
उत्तर
The given curve is y = 3x4 − 4x.
Then, the slope of the tangent to the given curve at x = 4 is given by,
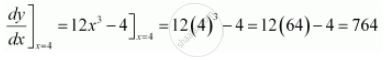
APPEARS IN
संबंधित प्रश्न
The equation of tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x – 5. Find the values of a and b.
Find the slope of the normal to the curve x = acos3θ, y = asin3θ at `theta = pi/4`
Find the equations of the tangent and normal to the given curves at the indicated points:
y = x3 at (1, 1)
Find the equation of the tangent line to the curve y = x2 − 2x + 7 which is perpendicular to the line 5y − 15x = 13.
Prove that the curves x = y2 and xy = k cut at right angles if 8k2 = 1. [Hint: Two curves intersect at right angle if the tangents to the curves at the point of intersection are perpendicular to each other.]
Find the equations of the tangent and the normal, to the curve 16x2 + 9y2 = 145 at the point (x1, y1), where x1 = 2 and y1 > 0.
Find the slope of the tangent and the normal to the following curve at the indicted point y = x3 − x at x = 2 ?
Find the points on the curve \[\frac{x^2}{9} + \frac{y^2}{16} = 1\] at which the tangent is parallel to x-axis ?
Find the points on the curve y = x3 where the slope of the tangent is equal to the x-coordinate of the point ?
Find the equation of the normal to y = 2x3 − x2 + 3 at (1, 4) ?
Find the equation of the tangent and the normal to the following curve at the indicated point y = x4 − bx3 + 13x2 − 10x + 5 at (0, 5) ?
Find the equation of the tangent and the normal to the following curve at the indicated point y = 2x2 − 3x − 1 at (1, −2) ?
Find the equation of the tangent and the normal to the following curve at the indicated point\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \text{ at }\left( a\cos\theta, b\sin\theta \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point xy = c2 at \[\left( ct, \frac{c}{t} \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated points x = asect, y = btant at t ?
The equation of the tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x − 5. Find the values of a and b ?
Find the equation of a normal to the curve y = x loge x which is parallel to the line 2x − 2y + 3 = 0 ?
Find the equation of the tangent to the curve x = sin 3t, y = cos 2t at
\[t = \frac{\pi}{4}\] ?
Find the equation of the tangents to the curve 3x2 – y2 = 8, which passes through the point (4/3, 0) ?
Find the angle of intersection of the following curve y = x2 and x2 + y2 = 20 ?
Show that the curves 4x = y2 and 4xy = k cut at right angles, if k2 = 512 ?
If the straight line xcos \[\alpha\] +y sin \[\alpha\] = p touches the curve \[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\] then prove that a2cos2 \[\alpha\] \[-\] b2sin2 \[\alpha\] = p2 ?
Write the coordinates of the point at which the tangent to the curve y = 2x2 − x + 1 is parallel to the line y = 3x + 9 ?
If the curves y = 2 ex and y = ae−x intersect orthogonally, then a = _____________ .
The slope of the tangent to the curve x = t2 + 3t − 8, y = 2t2 − 2t − 5 at the point (2, −1) is _____________ .
Find the equation of a tangent and the normal to the curve `"y" = (("x" - 7))/(("x"-2)("x"-3)` at the point where it cuts the x-axis
Find the angle of intersection of the curves y2 = x and x2 = y.
The point on the curve y2 = x, where the tangent makes an angle of `pi/4` with x-axis is ______.
Find an angle θ, 0 < θ < `pi/2`, which increases twice as fast as its sine.
Find the equation of the normal lines to the curve 3x2 – y2 = 8 which are parallel to the line x + 3y = 4.
At what points on the curve x2 + y2 – 2x – 4y + 1 = 0, the tangents are parallel to the y-axis?
The equation of normal to the curve 3x2 – y2 = 8 which is parallel to the line x + 3y = 8 is ______.
The equation of normal to the curve y = tanx at (0, 0) is ______.
The distance between the point (1, 1) and the tangent to the curve y = e2x + x2 drawn at the point x = 0
Tangent and normal are drawn at P(16, 16) on the parabola y2 = 16x, which intersect the axis of the parabola at A and B, respectively. If C is the centre of the circle through the points P, A and B and ∠CPB = θ, then a value of tan θ is:
Let `y = f(x)` be the equation of the curve, then equation of normal is
