Advertisements
Advertisements
प्रश्न
Find the differential equation all parabolas having a length of latus rectum 4a and axis is parallel to the axis.
Advertisements
उत्तर
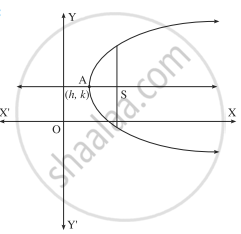
Let A(h, k) be the vertex of the parabola whose length of the latus rectum is 4a.
Then the equation of the parabola is
(y - k)2 = 4a(x - h), where h and k are arbitrary constants. Differentiating w.r.t. x, we get
`2("y - k") * "d"/"dx" ("y - k") = 4"a" "d"/"dx" ("x - h")`
∴ `2("y - k")("dy"/"dx" - 0) = "4a"(1 - 0)`
∴ `2("y - k")"dy"/"dx" = "4a"`
∴ `("y - k")"dy"/"dx" = "2a"` ...(1)
Differentiating again w.r.t. x, we get
`("y - k") * "d"/"dx" ("dy"/"dx") + "dy"/"dx" * "d"/"dx" ("y - k") = 0`
∴ `("y - k")("d"^2"y")/"dx"^2 + "dy"/"dx" * ("dy"/"dx" - 0) = 0`
∴ `("y - k")("d"^2"y")/"dx"^2 + ("dy"/"dx")^2 = 0`
∴ `"2a"/(("dy"/"dx")) * ("d"^2"y")/"dx"^2 + ("dy"/"dx")^2 = 0` ....[By (1)]
∴ `"2a" ("d"^2"y")/"dx"^2 + ("dy"/"dx")^3 = 0`
This is the required D.E.
APPEARS IN
संबंधित प्रश्न
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
y = A cos (log x) + B sin (log x)
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
(y - a)2 = 4(x - b)
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
y = a + `"a"/"x"`
Find the differential equation of the ellipse whose major axis is twice its minor axis.
Form the differential equation of family of lines parallel to the line 2x + 3y + 4 = 0.
Form the differential equation of all parabolas whose axis is the X-axis.
In the following example verify that the given expression is a solution of the corresponding differential equation:
xy = log y +c; `"dy"/"dx" = "y"^2/(1 - "xy")`
In the following example verify that the given expression is a solution of the corresponding differential equation:
y = `"a" + "b"/"x"; "x" ("d"^2"y")/"dx"^2 + 2 "dy"/"dx" = 0`
Solve the following differential equation:
`"dy"/"dx" = (1 + "y")^2/(1 + "x")^2`
Solve the following differential equation:
`"y" - "x" "dy"/"dx" = 0`
Solve the following differential equation:
`"dy"/"dx" = - "k",` where k is a constant.
Solve the following differential equation:
`2"e"^("x + 2y") "dx" - 3"dy" = 0`
For the following differential equation find the particular solution satisfying the given condition:
3ex tan y dx + (1 + ex) sec2 y dy = 0, when x = 0, y = π.
Choose the correct option from the given alternatives:
x2 + y2 = a2 is a solution of
Choose the correct option from the given alternatives:
The solution of `"dy"/"dx" + "y" = cos "x" - sin "x"`
The particular solution of `dy/dx = xe^(y - x)`, when x = y = 0 is ______.
In the following example verify that the given function is a solution of the differential equation.
`"x"^2 + "y"^2 = "r"^2; "x" "dy"/"dx" + "r" sqrt(1 + ("dy"/"dx")^2) = "y"`
In the following example verify that the given function is a solution of the differential equation.
`"xy" = "ae"^"x" + "be"^-"x" + "x"^2; "x" ("d"^2"y")/"dx"^2 + 2 "dy"/"dx" + "x"^2 = "xy" + 2`
In the following example verify that the given function is a solution of the differential equation.
`"x"^2 = "2y"^2 log "y", "x"^2 + "y"^2 = "xy" "dx"/"dy"`
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
(y - a)2 = b(x + 4)
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
y = `sqrt("a" cos (log "x") + "b" sin (log "x"))`
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
y = `"Ae"^(3"x" + 1) + "Be"^(- 3"x" + 1)`
Solve the following differential equation:
x dy = (x + y + 1) dx
Find the particular solution of the following differential equation:
`"dy"/"dx" - 3"y" cot "x" = sin "2x"`, when `"y"(pi/2) = 2`
Select and write the correct alternative from the given option for the question
General solution of `y - x ("d"y)/("d"x)` = 0 is
Find the differential equation of family of lines making equal intercepts on coordinate axes
Form the differential equation of family of standard circle
Find the differential equation of family of all ellipse whose major axis is twice the minor axis
Find the differential equation by eliminating arbitrary constants from the relation x2 + y2 = 2ax
Find the differential equation from the relation x2 + 4y2 = 4b2
The differential equation having y = (cos-1 x)2 + P (sin-1 x) + Q as its general solution, where P and Q are arbitrary constants, is
The family of curves y = `e^("a" sin x)`, where a is an arbitrary constant, is represented by the differential equation.
Find the differential equation of the family of all non-horizontal lines in a plane
Find the differential equation corresponding to the family of curves represented by the equation y = Ae8x + Be –8x, where A and B are arbitrary constants
Find the differential equation of the curve represented by xy = aex + be–x + x2
Choose the correct alternative:
The slope at any point of a curve y = f(x) is given by `("d"y)/("d"x) - 3x^2` and it passes through (-1, 1). Then the equation of the curve is
If `x^2 y^2 = sin^-1 sqrt(x^2 + y^2) + cos^-1 sqrt(x^2 + y^2)`, then `"dy"/"dx"` = ?
The differential equation of all lines perpendicular to the line 5x + 2y + 7 = 0 is ____________.
The differential equation representing the family of parabolas having vertex at origin and axis along positive direction of X-axis is ______.
The differential equation for all the straight lines which are at the distance of 2 units from the origin is ______.
If y = (tan–1 x)2 then `(x^2 + 1)^2 (d^2y)/(dx^2) + 2x(x^2 + 1) (dy)/(dx)` = ______.
The differential equation of all parabolas whose axis is Y-axis, is ______.
The differential equation of all circles passing through the origin and having their centres on the X-axis is ______.
The differential equation for a2y = log x + b, is ______.
If 2x = `y^(1/m) + y^(-1/m)`, then show that `(x^2 - 1) (dy/dx)^2` = m2y2
Form the differential equation whose general solution is y = a cos 2x + b sin 2x.
The differential equation whose solution represents the family \[x^{2}y=4e^{x}+c\], where c is an arbitrary constant, is
