Advertisements
Advertisements
Question
Find the differential equation all parabolas having a length of latus rectum 4a and axis is parallel to the axis.
Advertisements
Solution
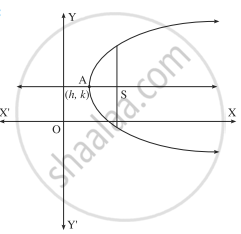
Let A(h, k) be the vertex of the parabola whose length of the latus rectum is 4a.
Then the equation of the parabola is
(y - k)2 = 4a(x - h), where h and k are arbitrary constants. Differentiating w.r.t. x, we get
`2("y - k") * "d"/"dx" ("y - k") = 4"a" "d"/"dx" ("x - h")`
∴ `2("y - k")("dy"/"dx" - 0) = "4a"(1 - 0)`
∴ `2("y - k")"dy"/"dx" = "4a"`
∴ `("y - k")"dy"/"dx" = "2a"` ...(1)
Differentiating again w.r.t. x, we get
`("y - k") * "d"/"dx" ("dy"/"dx") + "dy"/"dx" * "d"/"dx" ("y - k") = 0`
∴ `("y - k")("d"^2"y")/"dx"^2 + "dy"/"dx" * ("dy"/"dx" - 0) = 0`
∴ `("y - k")("d"^2"y")/"dx"^2 + ("dy"/"dx")^2 = 0`
∴ `"2a"/(("dy"/"dx")) * ("d"^2"y")/"dx"^2 + ("dy"/"dx")^2 = 0` ....[By (1)]
∴ `"2a" ("d"^2"y")/"dx"^2 + ("dy"/"dx")^3 = 0`
This is the required D.E.
APPEARS IN
RELATED QUESTIONS
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
Ax2 + By2 = 1
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
y2 = (x + c)3
Form the differential equation of all parabolas whose axis is the X-axis.
In the following example verify that the given expression is a solution of the corresponding differential equation:
xy = log y +c; `"dy"/"dx" = "y"^2/(1 - "xy")`
In the following example verify that the given expression is a solution of the corresponding differential equation:
y = `(sin^-1 "x")^2 + "c"; (1 - "x"^2) ("d"^2"y")/"dx"^2 - "x" "dy"/"dx" = 2`
In the following example verify that the given expression is a solution of the corresponding differential equation:
y = e-x + Ax + B; `"e"^"x" ("d"^2"y")/"dx"^2 = 1`
In the following example verify that the given expression is a solution of the corresponding differential equation:
y = `"a" + "b"/"x"; "x" ("d"^2"y")/"dx"^2 + 2 "dy"/"dx" = 0`
Solve the following differential equation:
`"dy"/"dx" = (1 + "y")^2/(1 + "x")^2`
Solve the following differential equation:
`"dy"/"dx" = - "k",` where k is a constant.
Solve the following differential equation:
`(cos^2y)/x dy + (cos^2x)/y dx` = 0
Solve the following differential equation:
`"y"^3 - "dy"/"dx" = "x"^2 "dy"/"dx"`
For the following differential equation find the particular solution satisfying the given condition:
`(e^y + 1) cos x + e^y sin x. dy/dx = 0, "when" x = pi/6,` y = 0
For the following differential equation find the particular solution satisfying the given condition:
`cos("dy"/"dx") = "a", "a" ∈ "R", "y"(0) = 2`
Reduce the following differential equation to the variable separable form and hence solve:
`"dy"/"dx" = cos("x + y")`
Choose the correct option from the given alternatives:
The differential equation of y = `"c"^2 + "c"/"x"` is
The integrating factor of linear differential equation `x dy/dx + 2y = x^2 log x` is ______.
In the following example verify that the given function is a solution of the differential equation.
`"y" = "e"^"ax" sin "bx"; ("d"^2"y")/"dx"^2 - 2"a" "dy"/"dx" + ("a"^2 + "b"^2)"y" = 0`
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
(y - a)2 = b(x + 4)
Form the differential equation of all the lines which are normal to the line 3x + 2y + 7 = 0.
Solve the following differential equation:
x dy = (x + y + 1) dx
Solve the following differential equation:
`"dx"/"dy" + "8x" = 5"e"^(- 3"y")`
Select and write the correct alternative from the given option for the question
General solution of `y - x ("d"y)/("d"x)` = 0 is
Select and write the correct alternative from the given option for the question
The solution of `("d"y)/("d"x)` = 1 is
Find the differential equation of family of lines making equal intercepts on coordinate axes
Find the general solution of `("d"y)/("d"x) = (1 + y^2)/(1 + x^2)`
Find the differential equation of family of all ellipse whose major axis is twice the minor axis
Verify y = log x + c is the solution of differential equation `x ("d"^2y)/("d"x^2) + ("d"y)/("d"x)` = 0
Find the differential equation from the relation x2 + 4y2 = 4b2
The differential equation having y = (cos-1 x)2 + P (sin-1 x) + Q as its general solution, where P and Q are arbitrary constants, is
Find the differential equation of the family of all non-vertical lines in a plane
Form the differential equation of all straight lines touching the circle x2 + y2 = r2
Find the differential equation of the family of all the parabolas with latus rectum 4a and whose axes are parallel to the x-axis
Find the differential equations of the family of all the ellipses having foci on the y-axis and centre at the origin
Find the differential equation of the curve represented by xy = aex + be–x + x2
Choose the correct alternative:
The slope at any point of a curve y = f(x) is given by `("d"y)/("d"x) - 3x^2` and it passes through (-1, 1). Then the equation of the curve is
The rate of disintegration of a radio active element at time t is proportional to its mass, at the time. Then the time during which the original mass of 1.5 gm. Will disintegrate into its mass of 0.5 gm. is proportional to ______.
If `x^2 y^2 = sin^-1 sqrt(x^2 + y^2) + cos^-1 sqrt(x^2 + y^2)`, then `"dy"/"dx"` = ?
The elimination of the arbitrary constant m from the equation y = emx gives the differential equation ______.
The differential equation representing the family of parabolas having vertex at origin and axis along positive direction of X-axis is ______.
For the curve C: (x2 + y2 – 3) + (x2 – y2 – 1)5 = 0, the value of 3y' – y3 y", at the point (α, α), α < 0, on C, is equal to ______.
The differential equation of all parabolas having vertex at the origin and axis along positive Y-axis is ______.
The differential equation for a2y = log x + b, is ______.
The differential equation whose solution represents the family \[x^{2}y=4e^{x}+c\], where c is an arbitrary constant, is
