Advertisements
Advertisements
प्रश्न
If θ is a positive acute angle such that sec θ = cosec 60°, find 2 cos2 θ – 1
उत्तर
We know that sec (90 – θ) = cosec2 θ
Sec θ = sec (90 – 60°)
On equating we get
Sec θ = sec 30°
𝜃 = 30°
To Find 2 cos2 θ – 1
`=> 2 xx cos^2 30^@ - 1` `[cos 30 = sqrt3/2]`
`=> 2 xx (sqrt3/2)^2 - 1`
`=> 2 xx 3/4 - 1`
`=> 3/2 - 1`
`= 1/2`
APPEARS IN
संबंधित प्रश्न
If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
If tan θ = `20/21` show that `((1-sin θ + cos θ))/((1+ sin θ +cos θ)) = 3/7`
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
If A = 450 , verify that:
(ii) cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
If sin A = `(7)/(25)`, find the value of : `"cos A" + (1)/"cot A"`
From the given figure, find the values of sin B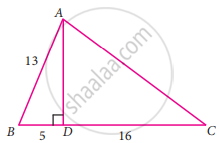
From the given figure, find the values of tan C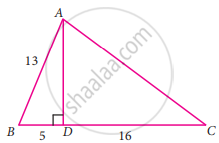
If A + B = 90°, cot B = `3/4` then tan A is equal to ______.
