Advertisements
Advertisements
प्रश्न
If tan = 0.75, find the other trigonometric ratios for A.
उत्तर
tan A = 0.75 = `(75)/(100) = (3)/(4) = "Perpendicular"/"Base"`
Hypotenuse
= `sqrt(("Perpendicular")^2 + ("Base")^2`
= `sqrt(3^2 + 4^2)`
= `sqrt(9 + 16)`
= `sqrt(25)`
= 5
sin A = `"Perpendicular"/"Hypotenuse" = (3)/(5)` = 0.6
cos A = `"Base"/"Hypotenuse" = (4)/(5)` = 0.8
cosecA = `(1)/"sin A" = (5)/(3)` = 1.66
sec A = `(1)/"cos A" = (5)/(4)` = 1.25
cost A = `(1)/"tan A" = (4)/(3)` = 1.33.
APPEARS IN
संबंधित प्रश्न
If θ is a positive acute angle such that sec θ = cosec 60°, find 2 cos2 θ – 1
In a ΔABC , ∠B = 90° , AB = 12 cm and BC = 5 cm Find
(i) cos A (ii) cosec A (iii) cos C (iv) cosec C
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
Evaluate:
sin600 cos300 + cos600 sin300
Given: 4 cot A = 3
find :
(i) sin A
(ii) sec A
(iii) cosec2A - cot2A.
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
In triangle ABC; ∠ABC = 90°, ∠CAB = x°, tan x° = `(3)/(4)` and BC = 15 cm. Find the measures of AB and AC.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosec C = `sqrt(10)`
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P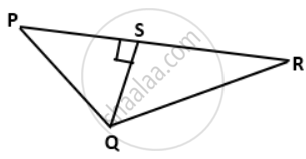
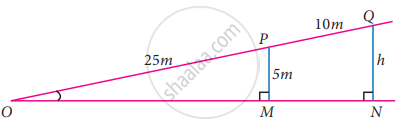
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)