Advertisements
Advertisements
प्रश्न
The function f(x) = 2x3 – 3x2 – 12x + 4, has ______.
पर्याय
Two points of local maximum
Two points of local minimum
One maxima and one minima
No maxima or minima
उत्तर
The function f(x) = 2x3 – 3x2 – 12x + 4, has one maxima and one minima.
Explanation:
We have f(x) = 2x3 – 3x2 – 12x + 4
f'(x) = 6x2 – 6x – 12
For local maxima and local minima f'(x) = 0
∴ 6x2 – 6x – 12 = 0
⇒ x2 – x – 2 = 0
⇒ x2 – 2x + x – 2 = 0
⇒ x(x – 2) + 1(x – 2) = 0
⇒ (x + 1)(x – 2) = 0
x = –1, 2 are the points of local maxima and local minima
Now f'(x) = 12x – 6
`"f''"(x)_(x = -1)` = 12(–1) – 6
= – 12 – 6
= – 18 < 0, maxima
`"f''"(x)_(x = 2)` = 12(2) – 6
= 24 – 6
= 18 > 0 minima
So, the function is maximum at x = –1 and minimum at x = 2
APPEARS IN
संबंधित प्रश्न
Find the maximum and minimum value, if any, of the function given by f(x) = |x + 2| − 1.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = x3 − 6x2 + 9x + 15
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
`f(x) = xsqrt(1-x), x > 0`
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is `tan^(-1) sqrt(2)`
Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to \[ \frac{2}{3} \] of the diameter of the sphere.
A given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order that the total surface area may be minimum the ratio of the length of the cylinder to the diameter of its semi-circular ends is \[\pi : (\pi + 2)\].
A rectangle is inscribed in a semicircle of radius r with one of its sides on the diameter of the semicircle. Find the dimensions of the rectangle to get the maximum area. Also, find the maximum area.
A ball is thrown in the air. Its height at any time t is given by h = 3 + 14t – 5t2. Find the maximum height it can reach.
A box with a square base is to have an open top. The surface area of the box is 192 sq cm. What should be its dimensions in order that the volume is largest?
Find the volume of the largest cylinder that can be inscribed in a sphere of radius ‘r’ cm.
Solve the following : Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is `(2"R")/sqrt(3)`. Also, find the maximum volume.
If f(x) = `x + 1/x, x ne 0`, then local maximum and x minimum values of function f are respectively.
The maximum and minimum values for the function f(x) = 4x3 - 6x2 on [-1, 2] are ______
The minimum value of the function f(x) = 13 - 14x + 9x2 is ______
If the sum of the lengths of the hypotenuse and a side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between them is `pi/3`
Find the points of local maxima, local minima and the points of inflection of the function f(x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
If y `= "ax - b"/(("x" - 1)("x" - 4))` has a turning point P(2, -1), then find the value of a and b respectively.
Find the area of the largest isosceles triangle having a perimeter of 18 meters.
Let P(h, k) be a point on the curve y = x2 + 7x + 2, nearest to the line, y = 3x – 3. Then the equation of the normal to the curve at P is ______.
The set of values of p for which the points of extremum of the function f(x) = x3 – 3px2 + 3(p2 – 1)x + 1 lie in the interval (–2, 4), is ______.
The greatest value of the function f(x) = `tan^-1x - 1/2logx` in `[1/sqrt(3), sqrt(3)]` is ______.
The maximum value of f(x) = `logx/x (x ≠ 0, x ≠ 1)` is ______.
The point in the interval [0, 2π], where f(x) = ex sin x has maximum slope, is ______.
Sum of two numbers is 5. If the sum of the cubes of these numbers is least, then find the sum of the squares of these numbers.
Complete the following activity to divide 84 into two parts such that the product of one part and square of the other is maximum.
Solution: Let one part be x. Then the other part is 84 - x
Letf (x) = x2 (84 - x) = 84x2 - x3
∴ f'(x) = `square`
and f''(x) = `square`
For extreme values, f'(x) = 0
∴ x = `square "or" square`
f(x) attains maximum at x = `square`
Hence, the two parts of 84 are 56 and 28.
The rectangle has area of 50 cm2. Complete the following activity to find its dimensions for least perimeter.
Solution: Let x cm and y cm be the length and breadth of a rectangle.
Then its area is xy = 50
∴ `y =50/x`
Perimeter of rectangle `=2(x+y)=2(x+50/x)`
Let f(x) `=2(x+50/x)`
Then f'(x) = `square` and f''(x) = `square`
Now,f'(x) = 0, if x = `square`
But x is not negative.
∴ `x = root(5)(2) "and" f^('')(root(5)(2))=square>0`
∴ by the second derivative test f is minimum at x = `root(5)(2)`
When x = `root(5)(2),y=50/root(5)(2)=root(5)(2)`
∴ `x=root(5)(2) "cm" , y = root(5)(2) "cm"`
Hence, rectangle is a square of side `root(5)(2) "cm"`
A box with a square base is to have an open top. The surface area of box is 147 sq. cm. What should be its dimensions in order that the volume is largest?
Sumit has bought a closed cylindrical dustbin. The radius of the dustbin is ‘r' cm and height is 'h’ cm. It has a volume of 20π cm3.
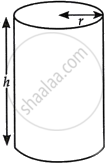
- Express ‘h’ in terms of ‘r’, using the given volume.
- Prove that the total surface area of the dustbin is `2πr^2 + (40π)/r`
- Sumit wants to paint the dustbin. The cost of painting the base and top of the dustbin is ₹ 2 per cm2 and the cost of painting the curved side is ₹ 25 per cm2. Find the total cost in terms of ‘r’, for painting the outer surface of the dustbin including the base and top.
- Calculate the minimum cost for painting the dustbin.
