Advertisements
Advertisements
प्रश्न
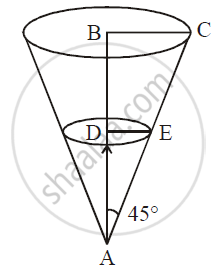
Water is dripping out from a conical funnel of semi-verticle angle `pi/4` at the uniform rate of `2 cm^2/sec`in the surface, through a tiny hole at the vertex of the bottom. When the slant height of the water level is 4 cm, find the rate of decrease of the slant height of the water.
उत्तर
Let r be the radius, h be the height and V be the volume of the funnel at any time t
`V = 1/3 pir^2h` ... (i)
Let I be the slant height of the funnel
Given: Semi-vertical angle = 45° in the triangle ADE:
`sin 45^@ = (DE)/(AE) => 1/sqrt2 = r/l`
`cos 45^@ = (AD)/(AE) => 1/sqrt2 = h/l`
`r = 1/sqrt2` and h = `1/sqrt2` ...(ii)
therefore the equation (i) can be rewritten as :
`V = 1/3 pi xx (I/sqrt2)^2 xx I/sqrt2 = pi/(3xx2xxsqrt2) xx I^3``
`V = pi/(6sqrt2) I^3` ...(iii)
Differentiate w.r.t. t :
`(dV)/(dt) = pi/(6sqrt2) xx 3l^2 xx (dl)/(dt)`
`(dv)/(dt) = pi/(2sqrt2) xx l^2 xx (dl)/(dt)`
`(dl)/(dt) = (2sqrt2)/(pil^2) xx (dV)/(dt)` ...(iv)
Since it is given that rate of change (decrease) of volume of water w.r.t. t is
`(dV)/(dt) = -2cm^3"/"sec`
therefore
`(dl)/(dt) = (2sqrt2)/(lambdal^2) xx (-2) = -(4sqrt2)/(lambdal^2)`
`(dl)/(dt)|_"at l = 4" = - (4sqrt2)/(pixx(4)^2) = - (sqrt2)/(4pi) "cm/sec"`
APPEARS IN
संबंधित प्रश्न
Find the intervals in which the function f(x) = 3x4 − 4x3 − 12x2 + 5 is
(a) strictly increasing
(b) strictly decreasing
Test whether the function is increasing or decreasing.
f(x) = `"x" -1/"x"`, x ∈ R, x ≠ 0,
Find the values of x for `y = [x(x - 2)]^2` is an increasing function.
Let I be any interval disjoint from (−1, 1). Prove that the function f given by `f(x) = x + 1/x` is strictly increasing on I.
Prove that the function given by f (x) = x3 – 3x2 + 3x – 100 is increasing in R.
Without using the derivative, show that the function f (x) = | x | is.
(a) strictly increasing in (0, ∞)
(b) strictly decreasing in (−∞, 0) .
Find the interval in which the following function are increasing or decreasing f(x) = 2x3 − 15x2 + 36x + 1 ?
Show that f(x) = cos x is a decreasing function on (0, π), increasing in (−π, 0) and neither increasing nor decreasing in (−π, π) ?
State when a function f(x) is said to be increasing on an interval [a, b]. Test whether the function f(x) = x2 − 6x + 3 is increasing on the interval [4, 6] ?
Find the intervals in which f(x) = (x + 2) e−x is increasing or decreasing ?
Prove that the following function is increasing on R f \[f\left( x \right) = 4 x^3 - 18 x^2 + 27x - 27\] ?
State whether f(x) = tan x − x is increasing or decreasing its domain ?
The function f(x) = x2 e−x is monotonic increasing when
f(x) = 2x − tan−1 x − log \[\left\{ x + \sqrt{x^2 + 1} \right\}\] is monotonically increasing when
Show that f(x) = cos x is a decreasing function on (0, π), increasing in (−π, 0) and neither increasing nor decreasing in (−π, π).
Prove that the function f : N → N, defined by f(x) = x2 + x + 1 is one-one but not onto. Find the inverse of f: N → S, where S is range of f.
Find the values of x for which the following functions are strictly decreasing:
f(x) = 2x3 – 3x2 – 12x + 6
Find the values of x for which f(x) = `x/(x^2 + 1)` is (a) strictly increasing (b) decreasing.
Find the value of x, such that f(x) is decreasing function.
f(x) = 2x3 - 15x2 - 144x - 7
For manufacturing x units, labour cost is 150 – 54x and processing cost is x2. Price of each unit is p = 10800 – 4x2. Find the values of x for which Revenue is increasing.
Let f(x) = x3 − 6x2 + 9𝑥 + 18, then f(x) is strictly decreasing in ______
Find the values of x for which the function f(x) = 2x3 – 6x2 + 6x + 24 is strictly increasing
The total cost function for production of articles is given as C = 100 + 600x – 3x2, then the values of x for which the total cost is decreasing is ______
The values of k for which the function f(x) = kx3 – 6x2 + 12x + 11 may be increasing on R are ______.
Let `"f (x) = x – cos x, x" in "R"`, then f is ____________.
The function which is neither decreasing nor increasing in `(pi/2,(3pi)/2)` is ____________.
The length of the longest interval, in which the function `3 "sin x" - 4 "sin"^3"x"` is increasing, is ____________.
The interval in which `y = x^2e^(-x)` is increasing with respect to `x` is
