Advertisements
Advertisements
Question
D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
Solution
Given: In a ΔABC, D, E and F are respectively the mid-points of the sides AB, BC and CA.
To prove: ΔABC is divided into four congruent triangles.
Proof: Since, ABC is a triangle and D, E and F are the mid-points of sides AB, BC and CA, respectively.
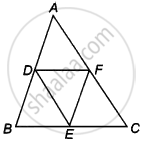
Then, AD = BD = `1/2`AB, BE = EC = `1/2`BC
And AF = CF = `1/2`AC
Now, using the mid-point theorem,
EF || AB and EF = `1/2`AB = AD = BD
ED || AC and ED = `1/2`AC = AF = CF
And DF || BC and DF = `1/2`BC = BE = CE
In ΔADF and ΔEFD,
AD = EF
AF = DE
And DF = FD ...[Common]
∴ ΔADF ≅ ΔEFD ...[By SSS congruence rule]
Similarly, ΔDEF ≅ ΔEDB
And ΔDEF ≅ ΔCFE
So, ΔABC is divided into four congruent triangles.
Hence proved.
APPEARS IN
RELATED QUESTIONS
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the
mid-points of the sides, in order, is a rectangle.
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
D and F are midpoints of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
- Prove that BDFE is a parallelogram
- Find AB, if EF = 4.8 cm.
In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.
Prove that: AC = 3AF.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔHEB ≅ ΔHFC
Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
