Advertisements
Advertisements
Question
Find cos(x − y), given that cos x = `- 4/5` with `pi < x < (3pi)/2` and sin y = `- 24/25` with `pi < y < (3pi)/2`
Solution
cos x = `- 4/5`
`pi < x < (3pi)/2`
⇒ x is in III quadrant
From ΔPQR,
PQ = `sqrt(5^2 - 4^2)`
= `sqrt(25 - 16)`
= `sqrt(9)`
= 3
Since x is in III quadrant
Both sin x and cos x are negative
∴ sin x = `- 3/5` and cos x = `- 4/5`
sin y = `- 24/25` and y is in III quadrant
Both sin y and cos y are negative
From ΔABC,
BC = `sqrt(25^2 - 24^2)`
= `sqrt(625 - 576)`
= `sqrt(49)`
= 7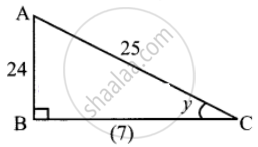
So, sin y = `- 24/25` = cos x cos y + sin x si y
= `(- 4/5)(- 7/25) + (-3/5)(- 24/25)`
= `28/125 + 72/125`
= `100/125`
= `4/5`
APPEARS IN
RELATED QUESTIONS
Find the values of `sin (-(11pi)/3)`
Find the value of the trigonometric functions for the following:
sec θ = `13/5`, θ lies in the IV quadrant
Show that `sin^2 pi/18 + sin^2 pi/9 + sin^2 (7pi)/18 + sin^2 (4pi)/9` = 2
If sin A = `3/5` and cos B = `9/41, 0 < "A" < pi/2, 0 < "B" < pi/2`, find the value of cos(A – B)
Find sin(x – y), given that sin x = `8/17` with 0 < x < `pi/2`, and cos y = `- 24/25`, x < y < `(3pi)/2`
Find a quadratic equation whose roots are sin 15° and cos 15°
Prove that sin 105° + cos 105° = cos 45°
If x cos θ = `y cos (theta + (2pi)/3) = z cos (theta + (4pi)/3)`. find the value of xy + yz + zx
Find the value of cos 2A, A lies in the first quadrant, when sin A = `4/5`
If θ is an acute angle, then find `cos (pi/4 + theta/2)`, when sin θ = `8/9`
Show that `cot(7 1^circ/2) = sqrt(2) + sqrt(3) + sqrt(4) + sqrt(6)`
Express the following as a product
cos 35° – cos 75°
Show that `(sin 8x cos x - sin 6x cos 3x)/(cos 2x cos x - sin 3x sin 4x)` = tan 2x
Show that `((cos theta -cos 3theta)(sin 8theta + sin 2theta))/((sin 5theta - sin theta) (cos 4theta - cos 6theta))` = 1
Prove that cos(30° – A) cos(30° + A) + cos(45° – A) cos(45° + A) = `cos 2"A" + 1/4`
If A + B + C = 180°, prove that sin2A + sin2B − sin2C = 2 sin A sin B cos C
If A + B + C = 180°, prove that `tan "A"/2 tan "B"/2 + tan "B"/2 tan "C"/2 + tan "C"/2 tan "A"/2` = 1
If A + B + C = 180°, prove that sin(B + C − A) + sin(C + A − B) + sin(A + B − C) = 4 sin A sin B sin C
