Advertisements
Advertisements
Question
If 4 cos2 x = 3 and x is an acute angle;
find the value of :
(i) x
(ii) cos2 x + cot2 x
(iii) cos 3x (iv) sin 2x
Solution
(i) 4 cos2x = 3
cos2x = `(3)/(4)`
cos x = `(sqrt3)/(2)`
x = 30°
(ii) cos2x + cot2x = cos230° + cot230°
= `(3)/(4) + 3`
= `(15)/(4)`
= 3`(3)/(4)`
(iii) cos 3x = cos3(30°) = cos 90° = 0
(iv) sin 2x = sin 2(30°) = sin60° = `(sqrt3)/(2)`
APPEARS IN
RELATED QUESTIONS
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
Solve the following equation for A, if 2 sin A = 1
Find the magnitude of angle A, if 2 cos2 A - 3 cos A + 1 = 0
Find the value of 'A', if 2cos 3A = 1
Find the value of 'A', if (1 - cosec A)(2 - sec A) = 0
If θ = 30°, verify that: 1 - sin 2θ = (sinθ - cosθ)2
If tan x° = `(5)/(12) . tan y° = (3)/(4)` and AB = 48m; find the length CD.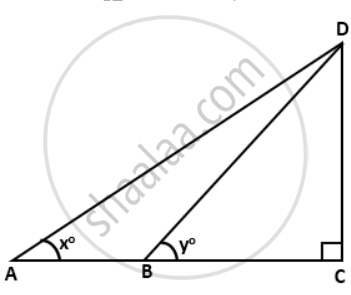
Evaluate the following: `(sin62°)/(cos28°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos84° + cosec69° - cot68°
Evaluate the following: `(5cot5° cot15° cot25° cot35° cot45°)/(7tan45° tan55° tan65° tan75° tan85°) + (2"cosec"12° "cosec"24° cos78° cos66°)/(7sin14° sin23° sec76° sec67°)`
