Advertisements
Advertisements
Question
If 5 cot θ = 12, find the value of : Cosec θ+ sec θ
Solution
Consider the diagram below :
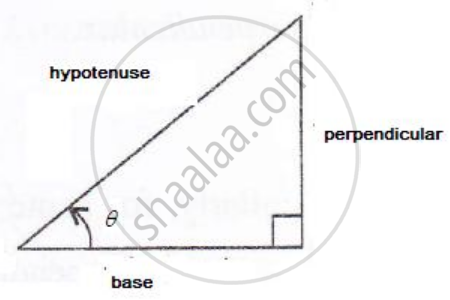
5cot θ = 12
cot θ = `(12)/(5)`
i.e.`"base"/"perpendicular" = (12)/(5)`
Therefore if length of base = 12x, length of perpendicular = 5x
Since
base2 + perpendicular2 = hypotenuse2 ...[ Using Pythagoras Theorem]
(12x)2 + (5x)2 = hypotenuse2
hypotenuse2 = 144x2 + 25x2 = 169x2
∴ hypotenuse = 13x
Now
cosec θ = `"hypotenuse"/"perpendicular" = (13x)/(5x) = (13)/(5)`
sec θ = `"hypotenuse"/"base" = (13x)/(12x) = (13)/(12)`
Therefore
cosec θ+sec θ
= `(13)/(5)+(13)/(12)`
= `(221)/(60)`
= `3(41)/(60)`
APPEARS IN
RELATED QUESTIONS
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If cos 2θ = sin 4θ where 2θ, 4θ are acute angles, find the value of θ.
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
Evaluate:
sin600 cos300 + cos600 sin300
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
Evaluate:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
If sin (A + B) = 1 and cos (A – B) = 1, 00 ≤ (A + B) ≤ 900 and A > B, then find A and B.
Given: cos A = `( 5 )/ ( 13 )`
Evaluate:
- `(sin "A "–cot "A") / (2 tan "A")`
- `cot "A" + 1/cos"A"`
In a right-angled triangle, it is given that A is an acute angle and tan A = `(5) /(12)`.
find the value of :
(i) cos A
(ii) sin A
(iii) ` (cosA+sinA)/(cosA– sin A)`
If sin A + cosec A = 2;
Find the value of sin2 A + cosec2 A.
