Advertisements
Advertisements
Question
If x = `(7 + 4sqrt(3))`, find the values of
`x^3 + (1)/x^3`
Solution
`x^3 + (1)/x^3`
`(x^3 + (1)/x^3) = (x + (1)/x)^3 - 3(x + (1)/x)` ----(1)
we will first find out `x + (1)/x`
`x + (1)/x = (7 + 4sqrt(3)) + (1)/((7 + 4sqrt(3))`
= `((7 + 4sqrt(3))^2 + 1)/((7 + 4sqrt(3))`
= `(49 + 48 + 56sqrt(3) + 1)/((7 + 4sqrt(3))`
= `(98 + 56sqrt(3))/((7 + 4sqrt(3))`
= `(14(7 + 4sqrt(3)))/((7 + 4sqrt(3))`
= 14
substitutingin (1)
`(x^3 + (1)/x^3) = (x + (1)/x)^3 -3(x + (1)/x)`
= (14)3 - 3 x 14
= 2744 - 42
= 2702
∴ `(x^3 + (1)/x^3)` = 2702
APPEARS IN
RELATED QUESTIONS
Rationalize the denominator.
`12/(4sqrt3 - sqrt 2)`
Rationalise the denominators of : `[ √3 + 1 ]/[ √3 - 1 ]`
Rationalise the denominators of : `[ sqrt3 - sqrt2 ]/[ sqrt3 + sqrt2 ]`
Simplify the following :
`sqrt(6)/(sqrt(2) + sqrt(3)) + (3sqrt(2))/(sqrt(6) + sqrt(3)) - (4sqrt(3))/(sqrt(6) + sqrt(2)`
In the following, find the values of a and b:
`(sqrt(11) - sqrt(7))/(sqrt(11) + sqrt(7)) = "a" - "b"sqrt(77)`
If x = `(4 - sqrt(15))`, find the values of:
`(x + (1)/x)^2`
If x = `((sqrt(3) + 1))/((sqrt(3) - 1)` and y = `((sqrt(3) - 1))/((sqrt(3) + 1)`, find the values of
x3 + y3
If x = `(1)/((3 - 2sqrt(2))` and y = `(1)/((3 + 2sqrt(2))`, find the values of
x2 + y2
Draw a line segment of length `sqrt3` cm.
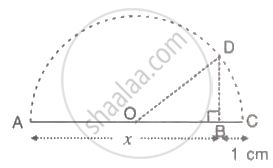
Using the following figure, show that BD = `sqrtx`.