Advertisements
Advertisements
Question
Write the mathematical equation for the first law of thermodynamics for:
Adiabatic process
Solution
First law of thermodynamic
ΔU = Q + W
For Adiabatic process
Q = 0
ΔU = W
APPEARS IN
RELATED QUESTIONS
The internal energy of an ideal gas decreases by the same amount as the work done by the system.
(a) The process must be adiabatic.
b) The process must be isothermal.
(c) The process must be isobaric.
(d) The temperature must decrease.
The internal energy of a gas is given by U = 1.5 pV. It expands from 100 cm3 to 200 cm3against a constant pressure of 1.0 × 105 Pa. Calculate the heat absorbed by the gas in the process.
A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
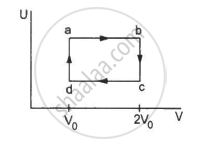
Find the change in the internal energy of 2 kg of water as it is heated from 0°C to 4°C. The specific heat capacity of water is 4200 J kg−1 K−1 and its densities at 0°C and 4°C are 999.9 kg m−3 and 1000 kg m−3 respectively. Atmospheric pressure = 105 Pa.
For an Isothermal process
ΔU is equal to ____________ work.
10 kg of four different gases (Cl2, CH4, O2, N2) expand isothermally and reversibly from 20 atm to 10 atm. The order of amount of work will be ____________.
Which of the following are TRUE for a reversible isothermal process?
(i) ∆U = 0
(ii) ∆H = 0
(iii) Q = W
(iv) ∆T = 0
A gas performs 0.320 kJ work on surrounding and absorbs 120 J of heat from the surrounding. Hence, change in internal energy is ______.
Change in internal energy, when 4 KJ of work is done on the system and 1 KJ heat is given out by the system, is:
Three copper blocks of masses M1, M2 and M3 kg respectively are brought into thermal contact till they reach equilibrium. Before contact, they were at T1, T2, T3 (T1 > T2 > T3). Assuming there is no heat loss to the surroundings, the equilibrium temprature T is (s is specific heat of copper)
Consider a cycle followed by an engine (Figure)
1 to 2 is isothermal
2 to 3 is adiabatic
3 to 1 is adiabatic
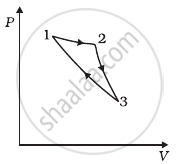
Such a process does not exist because ______.
- heat is completely converted to mechanical energy in such a process, which is not possible.
- mechanical energy is completely converted to heat in this process, which is not possible.
- curves representing two adiabatic processes don’t intersect.
- curves representing an adiabatic process and an isothermal process don’t intersect.
Is it possible to increase the temperature of a gas without adding heat to it? Explain.
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
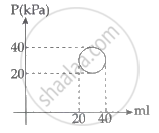
An electric appliance supplies 6000 J/min heat to the system. If the system delivers a power of 90 W. How long it would take to increase the internal energy by 2.5 × 103 J?
A soap bubble in vacuum has a radius of 3 cm and another soap bubble in vacuum has a radius of 4 cm. If the two bubbles coalesce under isothermal condition, then the radius of the new bubble is ______.
An ideal gas having pressure p, volume V and temperature T undergoes a thermodynamic process in which dW = 0 and dQ < 0. Then, for the gas ______.
A given system undergoes a change in which the work done by the system equals the decrease in its internal energy. The system must have undergone an ______.
104 J of work is done on a certain volume of a gas. If the gas releases 125 kJ of heat, calculate the change in internal energy of the gas.
If the adiabatic ratio for a gas is 5/3, find the molar specific heat capacity of the gas at (i) constant volume (ii) constant pressure.
In an adiabatic process, W = ______.
Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
Explain the formulation of first law of thrmodynamics.
Choose the correct relation with reason.
Define the isothermal process.
Define isochoric process
