HSC Science (General)
HSC Arts (English Medium)
HSC Science (Electronics)
HSC Science (Computer Science)
HSC Arts (Marathi Medium)
Academic Year: 2023-2024
Date & Time: 2nd March 2024, 11:00 am
Duration: 3h
Advertisements
General Instruction:
The question paper is divided into FOUR sections.
- Section A:
Q. 1 contains Eight multiple choice type of questions, each carrying Two marks.
Q. 2 contains Four very short answer type questions, each carrying One mark. - Section B: Q. 3 to Q. 14 contain Twelve short answer type questions, each carrying Two marks. (Attempt any Eight)
- Section C: Q. 15 to Q. 26 contains Twelve short answer type questions, each carrying Three marks. (Attempt any Eight)
- Section D: Q. 27 to Q. 34 contain Eight long answer type questions, each carrying Four marks. (Attempt any Five)
- Use of log table is allowed. Use of calculator is not allowed.
- Figures to the right indicate full marks.
- Use of graph paper is not necessary. Only rough sketch of graph is expected.
- For each multiple choice type of question; only the first attempt will be considered for evaluation.
- Start answer 10 each section on a new page.
The dual of statement t ∨ (p ∨ q) is ______.
c ∧ (p ∨ q)
c ∧ (p ∧ q)
t ∧ (p ∧ q)
t ∧ (p ∨ q)
Chapter: [0.011000000000000001] Mathematical Logic
The principle solutions of the equation cos θ = `1/2` are ______.
`π/6, (5π)/6`
`π/3, (5π)/3`
`π/6, (7π)/6`
`π/3, (2π)/3`
Chapter: [0.024] Definite Integration
If α, β, γ are direction angles of a line and α = 60°, β = 45°, then γ = ______.
30° or 90°
45° or 60°
90° or 130°
60° or 120°
Chapter: [0.015] Vectors
The perpendicular distance of the plane `bar r. (3 hat i + 4 hat j + 12 hat k) = 78` from the origin is ______.
4
5
6
8
Chapter: [0.016] Line and Plane
The slope of the tangent to the curve x = sin θ and y = cos 2θ at θ = `π/6` is ______.
`-2sqrt3`
`(-2)/sqrt3`
−2
`-1/2`
Chapter: [0.026000000000000002] Differential Equations
If `int_((-pi)/4) ^(pi/4) x^3 * sin^4 x dx` = k then k = ______.
1
2
4
0
Chapter: [0.024] Definite Integration
The integrating factor of linear differential equation `x dy/dx + 2y = x^2 log x` is ______.
`1/"x"`
k
`1/"n"^2`
x2
x
`1/x^2`
Chapter: [0.026000000000000002] Differential Equations
If the mean and variance of a binomial distribution are 18 and 12 respectively, then n = ______.
36
54
18
27
Chapter: [0.027999999999999997] Binomial Distribution
Write the following compound statement symbolically.
Nagpur is in Maharashtra and Chennai is in Tamil Nadu.
Chapter: [0.01] Mathematical Logic [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
Chapter: [0.015] Vectors
Evaluate:
`int1/(x^2 + 25)dx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
A particle is moving along the X-axis. Its acceleration at time t is proportional to its velocity at that time. Find the differential equation of the motion of the particle.
Chapter: [0.026000000000000002] Differential Equations
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
Chapter: [0.01] Mathematical Logic [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
Advertisements
Check whether the following matrix is invertible or not:
`[(cos theta, sin theta),(-sin theta, cos theta)]`
Chapter: [0.012] Matrics
In ΔABC, if a = 18, b = 24, c = 30 then find the values of sin `(A/2)`.
Chapter: [0.013000000000000001] Trigonometric Functions [0.03] Trigonometric Functions
Find k, if the sum of the slopes of the lines represented by x2 + kxy − 3y2 = 0 is twice their product.
Chapter: [0.013999999999999999] Pair of Straight Lines
If `bara, barb, barc` are the position vectors of the points A, B, C respectively and `5 bar a - 3 bar b - 2 bar c = bar 0`, then find the ratio in which the point C divides the line segment BA.
Chapter: [0.015] Vectors [0.07] Vectors
Find the vector equation of the line passing through the point having position vector `4hat i - hat j + 2hat"k"` and parallel to the vector `-2hat i - hat j + hat k`.
Chapter: [0.016] Line and Plane
Find `dy/dx`, if y = (log x)x.
Chapter: [0.021] Differentiation
Evaluate:
`int log x dx`
Chapter: [0.021] Differentiation
Evaluate the definite integral:
`int_0^(pi/2) cos^2 xdx`
Chapter: [0.15] Integration
Find the area of the region bounded by the curve y = x2, and the lines x = 1, x = 2, and y = 0.
Chapter: [0.025] Application of Definite Integration
Solve:
`1 + (dy)/(dx) = cosec (x + y)`; put x + y = u.
Chapter: [0.026000000000000002] Differential Equations
Find the probability distribution of number of heads in two tosses of a coin.
Chapter: [0.027000000000000003] Probability Distributions [0.19] Probability Distribution
Find the symbolic form of the given switching circuit. Construct its switching table and interpret your result.
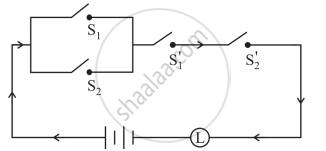
Chapter: [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
Prove the following:
`tan^-1(1/2) + tan^-1(1/3) = pi/(4)`
Chapter: [0.013000000000000001] Trigonometric Functions [0.03] Trigonometric Functions
In ΔABC, prove the following:
`(cos A)/a + (cos B)/b + (cos C)/c = (a^2 + b^2 + c^2)/(2abc)`
Chapter: [0.013000000000000001] Trigonometric Functions [0.03] Trigonometric Functions
Prove by vector method, that the angle subtended on semicircle is a right angle.
Chapter: [0.015] Vectors [0.07] Vectors
Advertisements
Find the shortest distance between the lines `barr = (4hati - hatj) + λ(hati + 2hatj - 3hatk)` and `barr = (hati - hatj -2hatk) + μ(hati + 4hatj - 5hatk)`
Chapter: [0.016] Line and Plane
Find the angle between the line `bar r = (hat i + 2hat j + hat k) + lambda(hat i + hat j + hat k)` and the plane `bar r *(2hat i + hat j + hat k) = 8`.
Chapter: [0.015] Vectors
If y = sin–1x, then show that `(1 - x^2) (d^2y)/(dx^2) - x * dy/dx` = 0
Chapter: [0.021] Differentiation
Find the approximate value of tan−1 (1.002).
[Given: π = 3.1416]
Chapter: [0.022000000000000002] Applications of Derivatives [0.14] Applications of Derivative
Prove that:
`int 1/(a^2 - x^2) dx = 1/2 a log ((a +x)/(a-x)) + c`
Chapter: [0.024] Definite Integration
Solve the following differential equation:
`x * dy/dx - y + x * sin(y/x) = 0`
Chapter: [0.026000000000000002] Differential Equations [0.17] Differential Equation
Find k, if the following function is p.d.f. of r.v.X:
f(x) = `{:(kx^2(1 - x)",", "for" 0 < x < 1),(0",", "otherwise"):}`
Chapter: [0.027000000000000003] Probability Distributions
A die is thrown 6 times. If ‘getting an odd number’ is a success, find the probability of 5 successes.
Chapter: [0.027999999999999997] Binomial Distribution
Solve the following system of equations by the method of reduction:
x + y + z = 6, y + 3z = 11, x + z = 2y.
Chapter: [0.012] Matrics
Prove that the acute angle θ between the lines represented by the equation ax2 + 2hxy+ by2 = 0 is tanθ = `|(2sqrt(h^2 - ab))/(a + b)|` Hence find the condition that the lines are coincident.
Chapter: [0.013999999999999999] Pair of Straight Lines
Find the volume of the parallelopiped whose vertices are A (3, 2, −1), B (−2, 2, −3) C (3, 5, −2) and D (−2, 5, 4).
Chapter: [0.015] Vectors [0.07] Vectors
Solve the following L.P.P. by graphical method:
Maximize: Z = 10x + 25y
subject to 0 ≤ x ≤ 3,
0 ≤ y ≤ 3,
x + y ≤ 5.
Also find the maximum value of z.
Chapter: [0.11] Linear Programming Problems
If x = f(t) and y = g(t) are differentiable functions of t, so that y is function of x and `(dx)/dt ≠ 0` then prove that `dy/(dx) = (dy/dt)/((dx)/dt)`. Hence find `dy/(dx)`, if x = at2, y = 2at.
Chapter: [0.021] Differentiation
A box with a square base is to have an open top. The surface area of box is 147 sq. cm. What should be its dimensions in order that the volume is largest?
Chapter: [0.022000000000000002] Applications of Derivatives [0.14] Applications of Derivative
Evaluate:
`int (5e^x)/((e^x + 1)(e^(2x) + 9)) dx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
Prove that:
`int_0^(2a)f(x)dx = int_0^af(x)dx + int_0^af(2a - x)dx`
Chapter: [0.026000000000000002] Differential Equations [0.17] Differential Equation
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 12th Standard Board Exam Mathematics and Statistics with solutions 2023 - 2024
Previous year Question paper for Maharashtra State Board 12th Standard Board Exam Maths and Stats-2024 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics and Statistics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 12th Standard Board Exam.
How Maharashtra State Board 12th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Mathematics and Statistics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
