Advertisements
Advertisements
प्रश्न
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sec B = `(15)/(12)`
उत्तर
sec B = `(15)/(12)`
sec B = `(1)/"cos B" = "Hypotenuse"/"Base" = (15)/(12)`
By Pythagoras theorem, we have
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ Perpendicular = `sqrt(("Hypotenuse")^2 - ("Base")^2`
⇒ Perpendicular
= `sqrt((15)^2 - (12)^2`
= `sqrt(225 - 144)`
= `sqrt(81)`
= 9
sinB = `"Perpendicular"/"Hypotenuse" = (9)/(15)`
tanB = `"Perpendicular"/"Base" = (9)/(12)`
cotB = `(1)/"tan B" = (12)/(9)`
cosecB = `(1)/"sinB" = (15)/(9)`
cos B = `"Base"/"Hypotenuse" = (12)/(15)`.
APPEARS IN
संबंधित प्रश्न
If A = B = 60°, verify that cos (A − B) = cos A cos B + sin A sin B
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
If Sec 4A = cosec (A – 20°) where 4A is an acute angle, find the value of A.
In the adjoining figure, ΔABC is right-angled at B and ∠A = 300. If BC = 6cm, find (i) AB, (ii) AC.
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ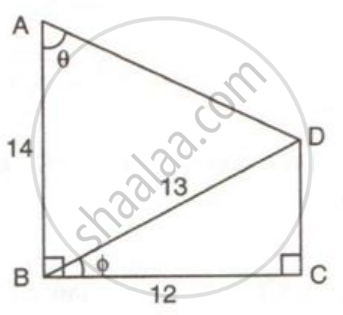
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
From the given figure, find the values of sec B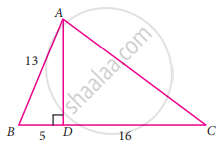
If 3 cot A = 2, then find the value of `(4sin"A" - 3cos"A")/(2sin"A" + 3cos"A")`
If A + B = 90°, cot B = `3/4` then tan A is equal to ______.
