Advertisements
Advertisements
प्रश्न
Prove that `2tan^(-1)(1/5)+sec^(-1)((5sqrt2)/7)+2tan^(-1)(1/8)=pi/4`
उत्तर
`2tan^(-1)(1/5)+sec^(-1)((5sqrt2)/7)+2tan^(-1)(1/8)`
`=2tan^(-1)(1/5)+tan^(-1)(sqrt(((5sqrt2)/7)^2-1))+2tan^(-1)(1/8) [`
`=2tan^(-1)(1/5)+tan^(-1)(1/7)+2tan^(-1)(1/8)`
`=2(tan^(-1)(1/5)+tan^(-1)(1/8))+tan^(-1)(1/7)`
`=tan^(-1)((1/5+1/8)/(1-(1/5)xx(1/8)))+tan^(-1)(1/7) [`
`=2 tan^(−1)(13/39)+tan^(−1)(1/7)`
`=2 tan^(−1)(1/3)+tan^(−1)(1/7)`
`= tan^(-1)((2/3)/(1-1/9))+tan^(−1)(1/7) [`
`=tan^(-1)(3/4)+tan^(-1)(1/7)`
`=tan^(-1)((3/4+1/7)/(1-(3/4)xx(1/7)))`
`=tan^(-1)(1)`
`=pi/4`
`=RHS`
Hence proved.
संबंधित प्रश्न
Prove that `tan^(-1)((6x-8x^3)/(1-12x^2))-tan^(-1)((4x)/(1-4x^2))=tan^(-1)2x;|2x|<1/sqrt3`
Find the value of `cot(tan^(-1) a + cot^(-1) a)`
if `sin(sin^(-1) 1/5 + cos^(-1) x) = 1` then find the value of x
Prove that:
`tan^(-1) 63/16 = sin^(-1) 5/13 + cos^(-1) 3/5`
Solve the following equation for x: `cos (tan^(-1) x) = sin (cot^(-1) 3/4)`
Prove that
\[2 \tan^{- 1} \left( \frac{1}{5} \right) + \sec^{- 1} \left( \frac{5\sqrt{2}}{7} \right) + 2 \tan^{- 1} \left( \frac{1}{8} \right) = \frac{\pi}{4}\] .
Solve for x : \[\cos \left( \tan^{- 1} x \right) = \sin \left( \cot^{- 1} \frac{3}{4} \right)\] .
Solve for x : `tan^-1 ((2-"x")/(2+"x")) = (1)/(2)tan^-1 ("x")/(2), "x">0.`
Find the value of `tan(sin^-1 3/5 + cot^-1 3/2)`
Prove that `sin^-1 3/5 - cos^-1 12/13 = sin^-1 16/65`
Solve: `sin^-1 5/x + sin^-1 12/x = pi/2`
Choose the correct alternative:
`sin^-1 (tan pi/4) - sin^-1 (sqrt(3/x)) = pi/6`. Then x is a root of the equation
Choose the correct alternative:
If `cot^-1(sqrt(sin alpha)) + tan^-1(sqrt(sin alpha))` = u, then cos 2u is equal to
Evaluate `cos[cos^-1 ((-sqrt(3))/2) + pi/6]`
`"sin" {2 "cos"^-1 ((-3)/5)}` is equal to ____________.
The domain of the function defind by f(x) `= "sin"^-1 sqrt("x" - 1)` is ____________.
`"tan"^-1 1/3 + "tan"^-1 1/5 + "tan"^-1 1/7 = "tan"^-1 1/8 =` ____________.
sin (tan−1 x), where |x| < 1, is equal to:
`"cos"^-1["cos"(2"cot"^-1(sqrt2 - 1))]` = ____________.
`"cos" (2 "tan"^-1 1/7) - "sin" (4 "sin"^-1 1/3) =` ____________.
`"sin"^-1 (1/sqrt2)`
`"sin"^-1 ((-1)/2)`
If `"sin"^-1 (1 - "x") - 2 "sin"^-1 ("x") = pi/2,` then x is equal to ____________.
The Government of India is planning to fix a hoarding board at the face of a building on the road of a busy market for awareness on COVID-19 protocol. Ram, Robert and Rahim are the three engineers who are working on this project. “A” is considered to be a person viewing the hoarding board 20 metres away from the building, standing at the edge of a pathway nearby. Ram, Robert and Rahim suggested to the firm to place the hoarding board at three different locations namely C, D and E. “C” is at the height of 10 metres from the ground level. For viewer A, the angle of elevation of “D” is double the angle of elevation of “C” The angle of elevation of “E” is triple the angle of elevation of “C” for the same viewer. Look at the figure given and based on the above information answer the following:
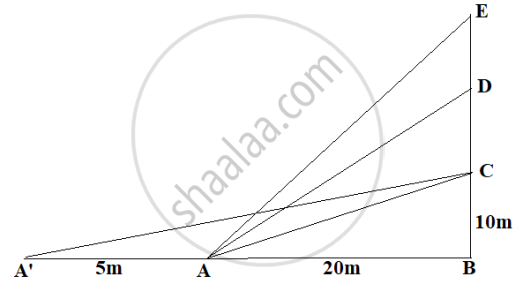
Measure of ∠EAB = ________.
`tan(2tan^-1 1/5 + sec^-1 sqrt(5)/2 + 2tan^-1 1/8)` is equal to ______.
The set of all values of k for which (tan–1 x)3 + (cot–1 x)3 = kπ3, x ∈ R, is the internal ______.
Write the following function in the simplest form:
`tan^-1 ((cos x - sin x)/(cos x + sin x)), (-pi)/4 < x < (3 pi)/4`
Solve:
sin–1(x) + sin–1(1 – x) = cos–1x.
