Advertisements
Advertisements
प्रश्न
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Advertisements
उत्तर
Let ABCD be a rectangle inscribed in the given circle of radius r having centre at O.
Let one side of the rectangle be c then the other side
`= sqrt((2r)^2 - x^2)`
`= sqrt(4r^2 - x^2)`
(∴ ∠ADC = ∠ABC = 90°; an angle in the semi-circle).
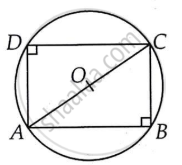
Let A be the corresponding area of the rectangle.
`A = xsqrt(4r^2 - x^2), 0 < x < 2r`
⇒ `(dA)/dx = (x(-2x))/(2 sqrt(4r^2 - x^2)) + sqrt(4r^2 - x^2)`
`= (2(2r^2 - x^2))/sqrt(4r^2 - x^2)`
For maximum / minimum area
`(dA)/dx = (2r^2 - x^2)/(sqrt(4r^2 - x^2)) = 0`
⇒ `x = sqrt2r` ...(∵ 0 < x < 2r)
Now,
`(d^2A)/dx^2 = (sqrt(4r^2 - x^2) (-4x) - (4r^2 - 2x^2) (1xx(-2x))/(2sqrt(4r^2 - x^2)))/((4r^2 - x^2))`
`= ((4r^2 - x^2) (-4x) + (4r^2 - 2x^2) x)/((4r^2 - x^2)^(3//2))`
`= (-12r^2x + 2x^3)/(4r^2 - x^2)^(3//2)`
`((d^2A)/dx^2)_(x = sqrt(2r))`
`= (-12r^2 (sqrt (2r)) + 2 (sqrt (2r))^3)/((2r^2)^(3//2)`
`= (4sqrt(2r^3) - 12 sqrt (2r^3))/(2 sqrt(2r^3))`
= 2 - 6 < 0
∴ Area is maximum at x = `sqrt(2r)`
∴ length of rectangle is `sqrt(2r)`
width of rectangle is `sqrt (4r^2 - x^2) = sqrt (2r)`
Hence the rectangle is a square of side `sqrt (2r)` for maximum area.
APPEARS IN
संबंधित प्रश्न
A telephone company in a town has 5000 subscribers on its list and collects fixed rent charges of Rs.3,000 per year from each subscriber. The company proposes to increase annual rent and it is believed that for every increase of one rupee in the rent, one subscriber will be discontinued. Find what increased annual rent will bring the maximum annual income to the company.
Find the maximum and minimum value, if any, of the following function given by g(x) = − |x + 1| + 3.
Find the maximum and minimum value, if any, of the following function given by h(x) = x + 1, x ∈ (−1, 1)
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = x3 − 6x2 + 9x + 15
Prove that the following function do not have maxima or minima:
f(x) = ex
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) =x^3, x in [-2,2]`
Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
Find two positive numbers x and y such that their sum is 35 and the product x2y5 is a maximum.
Find the maximum area of an isosceles triangle inscribed in the ellipse `x^2/ a^2 + y^2/b^2 = 1` with its vertex at one end of the major axis.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening
A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle.
Show that the minimum length of the hypotenuse is `(a^(2/3) + b^(2/3))^(3/2).`
Prove that the semi-vertical angle of the right circular cone of given volume and least curved surface is \[\cot^{- 1} \left( \sqrt{2} \right)\] .
A rod of 108 meters long is bent to form a rectangle. Find its dimensions if the area is maximum. Let x be the length and y be the breadth of the rectangle.
The volume of a closed rectangular metal box with a square base is 4096 cm3. The cost of polishing the outer surface of the box is Rs. 4 per cm2. Find the dimensions of the box for the minimum cost of polishing it.
Find the maximum and minimum of the following functions : f(x) = 2x3 – 21x2 + 36x – 20
Divide the number 30 into two parts such that their product is maximum.
Divide the number 20 into two parts such that sum of their squares is minimum.
Solve the following : Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/(3)`.
A rectangular sheet of paper has it area 24 sq. Meters. The margin at the top and the bottom are 75 cm each and the sides 50 cm each. What are the dimensions of the paper if the area of the printed space is maximum?
Max value of z equals 3x + 2y subject to x + y ≤ 3, x ≤ 2, -2x + y ≤ 1, x ≥ 0, y ≥ 0 is ______
The function y = 1 + sin x is maximum, when x = ______
Let f have second derivative at c such that f′(c) = 0 and f"(c) > 0, then c is a point of ______.
Find the points of local maxima, local minima and the points of inflection of the function f(x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
A telephone company in a town has 500 subscribers on its list and collects fixed charges of Rs 300/- per subscriber per year. The company proposes to increase the annual subscription and it is believed that for every increase of Re 1/- one subscriber will discontinue the service. Find what increase will bring maximum profit?
If x is real, the minimum value of x2 – 8x + 17 is ______.
Find all the points of local maxima and local minima of the function f(x) = (x - 1)3 (x + 1)2
If y = x3 + x2 + x + 1, then y ____________.
The area of a right-angled triangle of the given hypotenuse is maximum when the triangle is ____________.
The function `f(x) = x^3 - 6x^2 + 9x + 25` has
The maximum value of the function f(x) = `logx/x` is ______.
Let A = [aij] be a 3 × 3 matrix, where
aij = `{{:(1, "," if "i" = "j"),(-x, "," if |"i" - "j"| = 1),(2x + 1, "," "otherwise"):}`
Let a function f: R→R be defined as f(x) = det(A). Then the sum of maximum and minimum values of f on R is equal to ______.
Let f(x) = |(x – 1)(x2 – 2x – 3)| + x – 3, x ∈ R. If m and M are respectively the number of points of local minimum and local maximum of f in the interval (0, 4), then m + M is equal to ______.
A rectangle with one side lying along the x-axis is to be inscribed in the closed region of the xy plane bounded by the lines y = 0, y = 3x and y = 30 – 2x. The largest area of such a rectangle is ______.
The maximum value of z = 6x + 8y subject to constraints 2x + y ≤ 30, x + 2y ≤ 24 and x ≥ 0, y ≥ 0 is ______.
A straight line is drawn through the point P(3, 4) meeting the positive direction of coordinate axes at the points A and B. If O is the origin, then minimum area of ΔOAB is equal to ______.
Find the maximum and the minimum values of the function f(x) = x2ex.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) `= x sqrt(1 - x), 0 < x < 1`
Mrs. Roy designs a window in her son’s study room so that the room gets maximum sunlight. She designs the window in the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the window that will admit maximum sunlight into the room.
