Advertisements
Advertisements
Question
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Solution
Let ABCD be a rectangle inscribed in the given circle of radius r having centre at O.
Let one side of the rectangle be c then the other side
`= sqrt((2r)^2 - x^2)`
`= sqrt(4r^2 - x^2)`
(∴ ∠ADC = ∠ABC = 90°; an angle in the semi-circle).
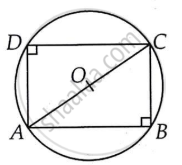
Let A be the corresponding area of the rectangle.
`A = xsqrt(4r^2 - x^2), 0 < x < 2r`
⇒ `(dA)/dx = (x(-2x))/(2 sqrt(4r^2 - x^2)) + sqrt(4r^2 - x^2)`
`= (2(2r^2 - x^2))/sqrt(4r^2 - x^2)`
For maximum / minimum area
`(dA)/dx = (2r^2 - x^2)/(sqrt(4r^2 - x^2)) = 0`
⇒ `x = sqrt2r` ...(∵ 0 < x < 2r)
Now,
`(d^2A)/dx^2 = (sqrt(4r^2 - x^2) (-4x) - (4r^2 - 2x^2) (1xx(-2x))/(2sqrt(4r^2 - x^2)))/((4r^2 - x^2))`
`= ((4r^2 - x^2) (-4x) + (4r^2 - 2x^2) x)/((4r^2 - x^2)^(3//2))`
`= (-12r^2x + 2x^3)/(4r^2 - x^2)^(3//2)`
`((d^2A)/dx^2)_(x = sqrt(2r))`
`= (-12r^2 (sqrt (2r)) + 2 (sqrt (2r))^3)/((2r^2)^(3//2)`
`= (4sqrt(2r^3) - 12 sqrt (2r^3))/(2 sqrt(2r^3))`
= 2 - 6 < 0
∴ Area is maximum at x = `sqrt(2r)`
∴ length of rectangle is `sqrt(2r)`
width of rectangle is `sqrt (4r^2 - x^2) = sqrt (2r)`
Hence the rectangle is a square of side `sqrt (2r)` for maximum area.
APPEARS IN
RELATED QUESTIONS
If `f'(x)=k(cosx-sinx), f'(0)=3 " and " f(pi/2)=15`, find f(x).
Find the maximum and minimum value, if any, of the following function given by f(x) = (2x − 1)2 + 3.
Find the maximum and minimum value, if any, of the following function given by h(x) = sin(2x) + 5.
Find the maximum and minimum value, if any, of the following function given by h(x) = x + 1, x ∈ (−1, 1)
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`g(x) = 1/(x^2 + 2)`
Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 − 72x − 18x2.
What is the maximum value of the function sin x + cos x?
Find the maximum value of 2x3 − 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [−3, −1].
Find the maximum and minimum values of x + sin 2x on [0, 2π].
Find two numbers whose sum is 24 and whose product is as large as possible.
Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
The maximum value of `[x(x −1) +1]^(1/3)` , 0 ≤ x ≤ 1 is ______.
Show that the surface area of a closed cuboid with square base and given volume is minimum, when it is a cube.
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when the depth of the tank is half of its width. If the cost is to be borne by nearby settled lower-income families, for whom water will be provided, what kind of value is hidden in this question?
Find the maximum and minimum of the following functions : f(x) = 2x3 – 21x2 + 36x – 20
Find the volume of the largest cylinder that can be inscribed in a sphere of radius ‘r’ cm.
If x + y = 3 show that the maximum value of x2y is 4.
Divide the number 20 into two parts such that their product is maximum
By completing the following activity, examine the function f(x) = x3 – 9x2 + 24x for maxima and minima
Solution: f(x) = x3 – 9x2 + 24x
∴ f'(x) = `square`
∴ f''(x) = `square`
For extreme values, f'(x) = 0, we get
x = `square` or `square`
∴ f''`(square)` = – 6 < 0
∴ f(x) is maximum at x = 2.
∴ Maximum value = `square`
∴ f''`(square)` = 6 > 0
∴ f(x) is maximum at x = 4.
∴ Minimum value = `square`
The function y = 1 + sin x is maximum, when x = ______
The maximum and minimum values for the function f(x) = 4x3 - 6x2 on [-1, 2] are ______
The sum of two non-zero numbers is 6. The minimum value of the sum of their reciprocals is ______.
Show that the function f(x) = 4x3 – 18x2 + 27x – 7 has neither maxima nor minima.
A telephone company in a town has 500 subscribers on its list and collects fixed charges of Rs 300/- per subscriber per year. The company proposes to increase the annual subscription and it is believed that for every increase of Re 1/- one subscriber will discontinue the service. Find what increase will bring maximum profit?
AB is a diameter of a circle and C is any point on the circle. Show that the area of ∆ABC is maximum, when it is isosceles.
The function `"f"("x") = "x" + 4/"x"` has ____________.
Read the following passage and answer the questions given below.
|
In an elliptical sport field the authority wants to design a rectangular soccer field with the maximum possible area. The sport field is given by the graph of `x^2/a^2 + y^2/b^2` = 1. |
- If the length and the breadth of the rectangular field be 2x and 2y respectively, then find the area function in terms of x.
- Find the critical point of the function.
- Use First derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.
OR
Use Second Derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.
Let A = [aij] be a 3 × 3 matrix, where
aij = `{{:(1, "," if "i" = "j"),(-x, "," if |"i" - "j"| = 1),(2x + 1, "," "otherwise"):}`
Let a function f: R→R be defined as f(x) = det(A). Then the sum of maximum and minimum values of f on R is equal to ______.
A rectangle with one side lying along the x-axis is to be inscribed in the closed region of the xy plane bounded by the lines y = 0, y = 3x and y = 30 – 2x. The largest area of such a rectangle is ______.
Find two numbers whose sum is 15 and when the square of one number multiplied by the cube of the other is maximum.
A metal wire of 36 cm long is bent to form a rectangle. Find its dimensions when its area is maximum.
Divide the number 100 into two parts so that the sum of their squares is minimum.
Find the point on the curve y2 = 4x, which is nearest to the point (2, 1).
A box with a square base is to have an open top. The surface area of box is 147 sq. cm. What should be its dimensions in order that the volume is largest?

