Advertisements
Advertisements
प्रश्न
Without using trigonometric tables, prove that:
cos 81° − sin 9° = 0
उत्तर
LHS = cos 81° − sin 9° = 0
= `cos (90^circ - 9^circ) - sin 9^circ`
= `sin 9^circ - sin 9^circ`
= 0
= RHS
APPEARS IN
संबंधित प्रश्न
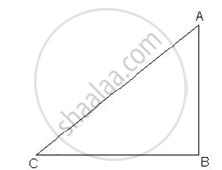
In the below given figure, a tower AB is 20 m high and BC, its shadow on the ground, is 20√3 m long. Find the sun’s altitude.
Evaluate without using trigonometric tables,
`sin^2 28^@ + sin^2 62^@ + tan^2 38^@ - cot^2 52^@ + 1/4 sec^2 30^@`
Without using trigonometric tables, evaluate :
`sec 11^circ/("cosec" 79^circ)`
Without using trigonometric tables, evaluate :
`tan 27^circ/cot 63^circ`
Without using trigonometric tables, evaluate :
`cot 38^circ/tan 52^circ`
Without using trigonometric tables, prove that:
tan266° − cot224° = 0
Without using trigonometric tables, prove that:
(sin 65° + cos 25°)(sin 65° − cos 25°) = 0
Without using trigonometric tables, prove that:
tan48° tan23° tan42° tan67° = 1
Prove that:
`(sin 70^circ)/(cos 20^circ) + ("cosec" 20^circ)/(sec 70^circ) - 2 cos 70^circ "cosec" 20^circ = 0`
Prove that:
\[\frac{\sin\theta}{\cos(90° - \theta)} + \frac{\cos\theta}{\sin(90° - \theta)} = 2\]
If sec2A = cosec(A - 42°), where 2A is an acute angle, then find the value of A.
If sec 4 A = cosec (A − 15°), where 4 A is an acute angle, find the value of A.
Given that `tan (θ_1 + θ_2) = (tan θ_1 + tan θ_2)/(1 - tan θ_1 tan θ_2)` Find (θ1 + θ2) when tan θ1 = `1/2 and tan θ_2 = 1/3`.
Solve : Sin2θ - 3sin θ + 2 = 0 .
Solve the following equation: `(cos^2θ - 3 cosθ + 2)/sin^2θ` = 1.
Using trigonometric table evaluate the following:
tan 25°45' + cot 45°25'.
Using trigonometric table evaluate the following:
sin 64°42' + cos 42°20'
`(sin 20°50' + tan 67°40')/(cos 32°20' - sin 15°10')`
