Advertisements
Advertisements
प्रश्न
Find the number of diagonals of (ii) a polygon of 16 sides.
उत्तर
A polygon of n sides has n vertices. By joining any two vertices we obtain either a side or a diagonal.
∴ Number of ways of selecting 2 out of 9 \[=^n C_2 = \frac{n\left( n - 1 \right)}{2}\]
Out of these lines, n lines are the sides of the polygon.
∴ Number of diagonals =\[\frac{n\left( n - 1 \right)}{2} - n = \frac{n\left( n - 3 \right)}{2}\]
There are 16 sides.
∴ Number of diagonals =\[\frac{16\left( 16 - 3 \right)}{2} = 104\]
APPEARS IN
संबंधित प्रश्न
Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.
How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER?
If the different permutations of all the letter of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E?
Compute:
In a class there are 27 boys and 14 girls. The teacher wants to select 1 boy and 1 girl to represent the class in a function. In how many ways can the teacher make this selection?
From Goa to Bombay there are two roots; air, and sea. From Bombay to Delhi there are three routes; air, rail and road. From Goa to Delhi via Bombay, how many kinds of routes are there?
How many different five-digit number licence plates can be made if
the first-digit cannot be zero, but the repetition of digits is allowed?
How many different numbers of six digits can be formed from the digits 3, 1, 7, 0, 9, 5 when repetition of digits is not allowed?
Serial numbers for an item produced in a factory are to be made using two letters followed by four digits (0 to 9). If the letters are to be taken from six letters of English alphabet without repetition and the digits are also not repeated in a serial number, how many serial numbers are possible?
Evaluate the following:
n + 1Cn
If 16Cr = 16Cr + 2, find rC4.
A student has to answer 10 questions, choosing at least 4 from each of part A and part B. If there are 6 questions in part A and 7 in part B, in how many ways can the student choose 10 questions?
In how many ways can a committee of 5 persons be formed out of 6 men and 4 women when at least one woman has to be necessarily selected?
Determine the number of 5 cards combinations out of a deck of 52 cards if there is exactly one ace in each combination.
In an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?
A parallelogram is cut by two sets of m lines parallel to its sides. Find the number of parallelograms thus formed.
Find the number of ways in which : (b) an arrangement, of four letters can be made from the letters of the word 'PROPORTION'.
A business man hosts a dinner to 21 guests. He is having 2 round tables which can accommodate 15 and 6 persons each. In how many ways can he arrange the guests?
5C1 + 5C2 + 5C3 + 5C4 +5C5 is equal to
In how many ways can a committee of 5 be made out of 6 men and 4 women containing at least one women?
Among 14 players, 5 are bowlers. In how many ways a team of 11 may be formed with at least 4 bowlers?
If n + 1C3 = 2 · nC2 , then n =
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is
There are 20 straight lines in a plane so that no two lines are parallel and no three lines are concurrent. Determine the number of points of intersection.
There are 8 doctors and 4 lawyers in a panel. Find the number of ways for selecting a team of 6 if at least one doctor must be in the team.
Find the value of 80C2
In how many ways a committee consisting of 3 men and 2 women, can be chosen from 7 men and 5 women?
In how many ways can a football team of 11 players be selected from 16 players? How many of them will include 2 particular players?
In how many ways can a football team of 11 players be selected from 16 players? How many of them will exclude 2 particular players?
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has no girls
15C8 + 15C9 – 15C6 – 15C7 = ______.
A committee of 6 is to be chosen from 10 men and 7 women so as to contain atleast 3 men and 2 women. In how many different ways can this be done if two particular women refuse to serve on the same committee ______.
Eighteen guests are to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on other side of the table. The number of ways in which the seating arrangements can be made is `(11!)/(5!6!) (9!)(9!)`.
To fill 12 vacancies there are 25 candidates of which 5 are from scheduled castes. If 3 of the vacancies are reserved for scheduled caste candidates while the rest are open to all, the number of ways in which the selection can be made is 5C3 × 20C9.
There are 3 books on Mathematics, 4 on Physics and 5 on English. How many different collections can be made such that each collection consists of:
| C1 | C2 |
| (a) One book of each subject; | (i) 3968 |
| (b) At least one book of each subject: | (ii) 60 |
| (c) At least one book of English: | (iii) 3255 |
There are 10 professors and 20 lecturers out of whom a committee of 2 professors and 3 lecturer is to be formed. Find:
| C1 | C2 |
| (a) In how many ways committee: can be formed | (i) 10C2 × 19C3 |
| (b) In how many ways a particular: professor is included | (ii) 10C2 × 19C2 |
| (c) In how many ways a particular: lecturer is included | (iii) 9C1 × 20C3 |
| (d) In how many ways a particular: lecturer is excluded | (iv) 10C2 × 20C3 |
There are 15 players in a cricket team, out of which 6 are bowlers, 7 are batsmen and 2 are wicketkeepers. The number of ways, a team of 11 players be selected from them so as to include at least 4 bowlers, 5 batsmen and 1 wicketkeeper, is ______.
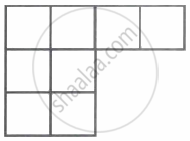
The no. of different ways, the letters of the word KUMARI can be placed in the 8 boxes of the given figure so that no row remains empty will be ______.
There are ten boys B1, B2, ...., B10 and five girls G1, G2, ...., G5 in a class. Then the number of ways of forming a group consisting of three boys and three girls, if both B1 and B2 together should not be the members of a group is ______.
