Advertisements
Advertisements
प्रश्न
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is `cos^(-1)(1/sqrt3)`
उत्तर
Let us consider the following variables:
h = height of the cone
l = slant height of the cone (given)
r = radius of the base of the cone
α = semi vertical angle of the cone
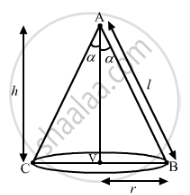
Let us assume that V' is the volume of the cone which has to be maximised.
We know that
`V' = 1/3πr^2h ...(1)`
From the figure, we have:
`l^2=r^2+h^2⇒l^2−h^2=r^2`
On substituting the value of r2 in equation (1), we get:
`V' = 1/3π(l^2−h^2)h=1/3π(l^2h−h^3) `
On differentiating with respect to h, we get:
`dV'/dh=1/3π(l^2−3h^2) ...(2)`
For maximum volume of V, let us put `(dV')/(dh)=0.`
So, from equation (2), we have:
`1/3π(l^2−3h^2)=0⇒h=l/sqrt3 (∵ h,l >0)`
Again, differentiating equation (2) with respect to h, we get:
`(d^2V'/dh^2)=1/3π(−6h)=−2πh`
`∴ ((d^2V')/(dh^2))_(h=l/sqrt3)=−2πl/sqrt3<0`
Thus, the volume of the cone is maximum at
`h=l/sqrt3`
From the figure, we have:
`cosα =h/l⇒cosα =l/lsqrt3=1/sqrt3`
`⇒α=cos^(−1)(1/sqrt3)`
∴ The semi-vertical angle is
`cos^(−1)(1/sqrt3). `
संबंधित प्रश्न
If the function f(x)=2x3−9mx2+12m2x+1, where m>0 attains its maximum and minimum at p and q respectively such that p2=q, then find the value of m.
Differentiate the following functions from first principles x2ex ?
Differentiate \[\sqrt{\frac{a^2 - x^2}{a^2 + x^2}}\] ?
Differentiate (log sin x)2 ?
Differentiate \[\sin \left( \frac{1 + x^2}{1 - x^2} \right)\] ?
Differentiate \[\frac{3 x^2 \sin x}{\sqrt{7 - x^2}}\] ?
Differentiate \[\frac{\sqrt{x^2 + 1} + \sqrt{x^2 - 1}}{\sqrt{x^2 + 1} - \sqrt{x^2 - 1}}\] ?
Differentiate \[\log \sqrt{\frac{x - 1}{x + 1}}\] ?
Differentiate \[\sin^{- 1} \left\{ \frac{\sqrt{1 + x} + \sqrt{1 - x}}{2} \right\}, 0 < x < 1\] ?
Differentiate \[\sin^{- 1} \left( \frac{1 - x^2}{1 + x^2} \right) + \sec^{- 1} \left( \frac{1 + x^2}{1 - x^2} \right), x \in R\] ?
Differentiate \[x^{\cos^{- 1} x}\] ?
Differentiate \[\sin \left( x^x \right)\] ?
Differentiate \[x^{\sin^{- 1} x}\] ?
If \[x^x + y^x = 1\], prove that \[\frac{dy}{dx} = - \left\{ \frac{x^x \left( 1 + \log x \right) + y^x \cdot \log y}{x \cdot y^\left( x - 1 \right)} \right\}\] ?
If \[y^x + x^y + x^x = a^b\] ,find \[\frac{dy}{dx}\] ?
Find \[\frac{dy}{dx}\] , when \[x = \cos^{- 1} \frac{1}{\sqrt{1 + t^2}} \text{ and y } = \sin^{- 1} \frac{t}{\sqrt{1 + t^2}}, t \in R\] ?
Differentiate \[\cos^{- 1} \left( 4 x^3 - 3x \right)\] with respect to \[\tan^{- 1} \left( \frac{\sqrt{1 - x^2}}{x} \right), \text{ if }\frac{1}{2} < x < 1\] ?
If \[y = \log_a x, \text{ find } \frac{dy}{dx} \] ?
If \[x = 3\sin t - \sin3t, y = 3\cos t - \cos3t \text{ find }\frac{dy}{dx} \text{ at } t = \frac{\pi}{3}\] ?
If \[y = \left( 1 + \frac{1}{x} \right)^x , \text{ then} \frac{dy}{dx} =\] ____________ .
Find the second order derivatives of the following function x3 log x ?
If x = a (θ − sin θ), y = a (1 + cos θ) prove that, find \[\frac{d^2 y}{d x^2}\] ?
If y = tan−1 x, show that \[\left( 1 + x^2 \right) \frac{d^2 y}{d x^2} + 2x\frac{dy}{dx} = 0\] ?
Find \[\frac{d^2 y}{d x^2}\] where \[y = \log \left( \frac{x^2}{e^2} \right)\] ?
\[\text { If x } = \cos t + \log \tan\frac{t}{2}, y = \sin t, \text { then find the value of } \frac{d^2 y}{d t^2} \text { and } \frac{d^2 y}{d x^2} \text { at } t = \frac{\pi}{4} \] ?
\[\text { If y } = x^n \left\{ a \cos\left( \log x \right) + b \sin\left( \log x \right) \right\}, \text { prove that } x^2 \frac{d^2 y}{d x^2} + \left( 1 - 2n \right)x\frac{d y}{d x} + \left( 1 + n^2 \right)y = 0 \] Disclaimer: There is a misprint in the question. It must be
\[x^2 \frac{d^2 y}{d x^2} + \left( 1 - 2n \right)x\frac{d y}{d x} + \left( 1 + n^2 \right)y = 0\] instead of 1
\[x^2 \frac{d^2 y}{d x^2} + \left( 1 - 2n \right)\frac{d y}{d x} + \left( 1 + n^2 \right)y = 0\] ?
\[\text { If } y = \left( x + \sqrt{1 + x^2} \right)^n , \text { then show that }\]
\[\left( 1 + x^2 \right)\frac{d^2 y}{d x^2} + x\frac{dy}{dx} = n^2 y .\]
If p, q, r, s are real number and pr = 2(q + s) then for the equation x2 + px + q = 0 and x2 + rx + s = 0 which of the following statement is true?
