Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
Options
70°
100°
125°
150°
Solution
70°
It is given that ABCD is cyclic quadrilateral ∠ADB = 90° and ∠DCA = 80°. We have to find ∠DAB
We have the following figure regarding the given information
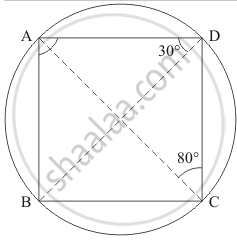
∠BDA = ∠BCA = 30° (Angle in the same segment are equal)
Now, since ABCD is a cyclic quadrilateral
So, ∠DAB + ∠BCD = 180°
`angleDAB + angleBCA + angleDCA` = 180°
`angleDAB ` + 30° + 80° = 180°
`angleDAB` = 180° - 110°
`angleDAB ` = 70 °
APPEARS IN
RELATED QUESTIONS
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that a cyclic parallelogram is a rectangle.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
Two chords AB and CD of lengths 5 cm 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
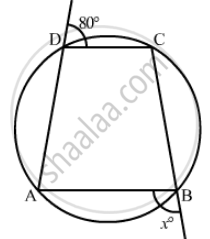
In the given figure, ABCD is a cyclic quadrilateral. Find the value of x.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
