Advertisements
Advertisements
Question
Evaluate the following :
sin 35° sin 55° − cos 35° cos 55°
Solution
We find sin 35° sin 55° − cos 35° cos 55°
Since `sin(90^@ - theta) = cos theta and cos (90^@ - theta) = sin theta`
`sin 35^@ sin 55^@- cos 35^@ cos 55^@ = sin (90^@ - 55^@)sin 55^@ - cos(90^@ - 55^@)cos 55^@`
`= cos 55^@ sin 55^@ - sin 55^@ cos 55^@`
= 1 - 1
= 0
So value of `sin 35^@ sin 55^@ - cos 35^@ cos 55^@` is 0
APPEARS IN
RELATED QUESTIONS
An equilateral triangle is inscribed in a circle of radius 6 cm. Find its side.
State whether the following is true or false. Justify your answer.
The value of cos θ increases as θ increases.
Evaluate the following :
`tan 10^@/cot 80^@`
Express each one of the following in terms of trigonometric ratios of angles lying between
0° and 45°
Sin 59° + cos 56°
Prove that:
sin 60° = 2 sin 30° cos 30°
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratio: cos 45°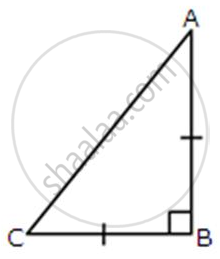
Without using tables, evaluate the following: cosec330° cos60° tan345° sin290° sec245° cot30°.
If sin(A - B) = sinA cosB - cosA sinB and cos(A - B) = cosA cosB + sinA sinB, find the values of sin15° and cos15°.
If sin(A - B) = `(1)/(2)` and cos(A + B) = `(1)/(2)`, find A and B.
Prove the following:
`(sqrt(3) + 1) (3 - cot 30^circ)` = tan3 60° – 2 sin 60°
