Advertisements
Advertisements
Question
Explain the phenomena of surface tension on the basis of molecular theory.
Solution
Molecular theory of surface tension:
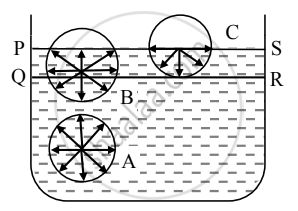
- Let PQRS = Surface film of liquid in a container containing liquid. PS is the free surface of the liquid and QR is the inner layer parallel to PS at distance equal to the range of molecular force.
- Now consider three molecules A, B, and C in a liquid in a vessel such that molecule A is well inside the liquid, molecule B within the surface film, and molecule C is on the surface of the liquid as shown in the figure.
- The sphere of influence of molecule A is entirely inside the liquid. As a result, molecule A is acted upon by equal cohesive forces in all directions. Thus, the net cohesive force acting on molecule A is zero.
- For molecule B, a large part of its sphere of influence is inside the liquid and a smaller part is outside the surface (in the air). The adhesive force acting on molecule B due to air molecules above it and within its sphere of influence is weak compared to the strong downward cohesive force acting on the molecule. As a result, molecule B gets attracted inside the liquid.
- For molecule C, half of the sphere of influence is in air and half is in liquid. As the density of air is much less than that of liquid, the number of air molecules within the sphere of influence of molecule C above the free surface of the liquid is much less than the numbers of liquid molecules within the sphere of influence that lies within the liquid. Thus, the adhesive force due to the air molecules acting on molecule C is weak compared to the cohesive force acting on the molecule. As a result, molecule C also gets attracted inside the liquid.
- Thus, all molecules in the surface film are acted upon by an unbalanced net cohesive force directed into the liquid. Therefore, the molecules in the surface film are pulled inside the liquid. This minimizes the total number of molecules in the surface film. As a result, the surface film remains under tension. The surface film of a liquid behaves like a stretched elastic membrane. This tension is known as surface tension and the force due to it acts tangential to the free surface of a liquid.
RELATED QUESTIONS
Define the angle of contact.
'n' droplets of equal size of radius r coalesce to form a bigger drop of radius R. The energy liberated is equal to...................
(T =Surface tension of water)
`(a) 4piR^2T[n^(1/3)-1]`
`(b) 4pir^2T[n^(1/3)-1]`
`(c) 4piR^2T[n^(2/3)-1]`
`(d)4 pir^2T[n^(2/3)-1]`
Explain why Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Explain why Water with detergent dissolved in it should have small angles of contact.
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10–2 N m–1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m–1. Density of mercury = 13.6 × 103 kg m–3
Define surface tension and surface energy.
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
A big drop of radius R is formed from 1000 droplets of water. The radius of a droplet will be _______
A) 10 R
B) R/10
C) R/100
D) R/1000
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of soap solution is 30 dyne/cm. (Π = 3.142).
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
The contact angle between water and glass is 0°. When water is poured in a glass to the maximum of its capacity, the water surface is convex upward. The angle of contact in such a situation is more than 90°. Explain.
A uniform vertical tube of circular cross section contains a liquid. The contact angle is 90°. Consider a diameter of the tube lying in the surface of the liquid. The surface to the right of this diameter pulls the surface on the left of it. What keeps the surface on the left in equilibrium?
If water in one flask and castor oil in other are violently shaken and kept on a table, which will come to rest earlier?
If two soap bubbles of different radii are connected by a tube,
The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
A liquid is contained in a vertical tube of semicircular cross section. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary.
(a) The surface tension of the liquid must be zero.
(b) The contact angle must be 90°.
(c) The surface tension may be zero.
(d) The contact angle may be 90°.
Find the excess pressure inside (a) a drop of mercury of radius 2 mm (b) a soap bubble of radius 4 mm and (c) an air bubble of radius 4 mm formed inside a tank of water. Surface tension of mercury, soap solution and water are 0.465 N m−1, 0.03 N m−1 and 0.076 N m−1 respectively.
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
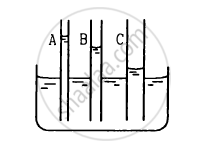
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
A drop of mercury of radius 2 mm is split into 8 identical droplets. Find the increase in surface energy. Surface tension of mercury = 0.465 J m−2.
Find the force exerted by the water on a 2 m2 plane surface of a large stone placed at the bottom of a sea 500 m deep. Does the force depend on the orientation of the surface?
A metal piece of mass 160 g lies in equilibrium inside a glass of water. The piece touches the bottom of the glass at a small number of points. If the density of the metal is 8000 kg/m3, find the normal force exerted by the bottom of the glass on the metal piece.

A ferry boat has internal volume 1 m3 and weight 50 kg.(a) Neglecting the thickness of the wood, find the fraction of the volume of the boat immersed in water.(b) If a leak develops in the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly ______.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Twenty-seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m.
Water rises to a height of 20 mm in a capillary tube. If the radius made 1/3rd of its previous value, to what height will the water now rise in the tube?
How does the friction arise between the surfaces of two bodies in relative motion?
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
Mention the S.I unit and dimension of surface tension.
Define the angle of contact for a given pair of solid and liquid.
A drop of oil placed on the surface of water spreads out. But a drop of water place on oil contracts to a spherical shape. Why?
Why coffee runs up into a sugar lump (a small cube of sugar) when one corner of the sugar lump is held in the liquid?
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
The excess of pressure, due to surface tension, on a spherical liquid drop of radius 'R' is proportional to ______.
A large number of liquid drops each of radius 'r' coalesce to form a big drop of radius 'R'. The energy released in the process in converted into kinetic energy of the big drop. The speed of the big drop is ______. (T = surface tension of liquid, p = density of liquid)
Soap solution is used for cleaning dirty clothes because ______.
The wear and tear in the machine part is due to ______.
For a surface molecule ______.
- the net force on it is zero.
- there is a net downward force.
- the potential energy is less than that of a molecule inside.
- the potential energy is more than that of a molecule inside.
Eight droplets of water each of radius 0.2 mm coalesce into a single drop. Find the decrease in the surface area.
Two narrow bores of diameter 5.0 mm and 8.0 mm are joined together to form a U-shaped tube open at both ends. If this U-tube contains water, what is the difference in the level of the two limbs, of the tube?
[Take surface tension of water T = 7.3 × 10-2 Nm-1, angle of contact = 0, g = 10 ms-2 and density of water = 1.0 × 103 kgm-3]
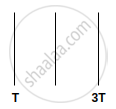
We have three identical perfectly black plates. The temperatures of first and third plate is T and 3T. What is the temperature of second plate if system is in equilibrium?
The surface tension of a soap solution is T. The work done in blowing a soap bubble of diameter d to that of a diameter 2d is ______.
A liquid drop of density ρ is floating half immersed in a liquid of density d. The diameter of the liquid drop is ______.
(ρ > d, g = acceleration due to gravity, T = surface tension)
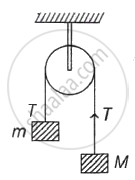
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
Work done to blow a bubble of volume V is W. The work done in blowing a bubble of volume 2V will be ______.
The surface tension of soap solution is 25 × 10-3 Nm-1. The excess of pressure inside a soap bubble of diameter 1 cm is ______.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
