Advertisements
Advertisements
Question
Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
sec 76° + cosec 52°
Solution
We know that `sec(90^@ - theta) = cosec theta` and `cosec (90^@) = sin theta` So
`sec 76^@ + cosec 52^@ = sec(90^@ - 14^@) + cosec (90^@ - 38^@)`
`= cosec14^@ + sec 38^@`
APPEARS IN
RELATED QUESTIONS
sin 2A = 2 sin A is true when A = ______.
Express cos 75° + cot 75° in terms of angles between 0° and 30°.
Evaluate: `sin 18^@/cos 72^@ + sqrt3 [tan 10° tan 30° tan 40° tan 50° tan 80°]`
Without using trigonometric tables, prove that:
cos54° cos36° − sin54° sin36° = 0
Prove that:
cos 30° . cos 60° - sin 30° . sin 60° = 0
Prove that:
`((tan60° + 1)/(tan 60° – 1))^2 = (1+ cos 30°) /(1– cos 30°) `
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios: tan 45°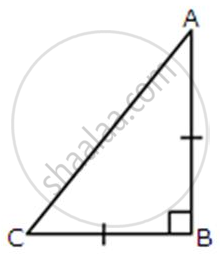
If A = 30o, then prove that :
2 cos2 A - 1 = 1 - 2 sin2A
Without using tables, evaluate the following: sec30° cosec60° + cos60° sin30°.
Without using table, find the value of the following: `(tan^2 60° + 4cos^2 45° + 3sec^2 30° + 5cos90°)/(cosec30° + sec60° - cot^2 30°)`
