Question

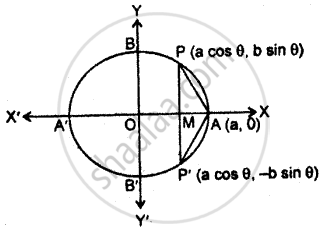
Find the maximum area of an isosceles triangle inscribed in the ellipse  `x^2/ a^2 + y^2/b^2 = 1` with its vertex at one end of the major axis.

Answer 1

Ellipse, `x^2/a^2 + y^2/b^2 = 1`

Let P be a point (a cos θ, b sin θ) on the ellipse. APP' is an isosceles triangle.

PP' intersects the axis AA' of the ellipse at point M.

Area of ​​∆APP' A = `1/2 PP' xx AM`

`= 1/2 (2 b sin theta) xx (a - a cos theta)`            ...[∵ PP' = 2 PM = 2b sin θ and AM = OA - OM = a - a cos θ]

`= 1/2 "ab" xx 2 sin theta (1 - cos theta)`

= ab sin θ (a - a cos θ)

= ab (sin θ - sin θ cos θ)

`= "ab"(sin θ - 1/2 * 2 sin θ cos θ)`

`= "ab" (sin theta - 1/2 sin 2 theta)`

On differentiating with respect to θ,

`(dA)/(d theta) = ab (cos theta - cos 2 theta)`

For highest to lowest, `(dA)/(d theta) = 0`

∴ ab(cos θ - cos 2θ) = 0

⇒ cos 2θ = cos θ

⇒ 2θ = 2π - θ

⇒ θ = `(2pi)/3`

Now, `(d^2A)/(d theta^2) = ab (- sin theta + 2 sin 2 theta)`

At, `theta = (2pi)/3 (d^2A)/(d theta^2) = ab (- sin  (2pi)/3 + 2 sin  (4pi)/3)`

`= ab [- (sqrt3/2) + 2 (- sqrt3/2)]`

`= ab (- sqrt3/2 - (2sqrt3)/2)`

`= (- 3 sqrt3)/2 ab < 0`

⇒ A is maximum when `theta = (2pi)/3 = 120^circ`

Maximum value of a = `ab (sin 120^circ - 1/2 sin 240^circ)`

`= ab [sqrt3/2 - 1/2 (- sqrt3/2)]`

`= ab(sqrt3/2 + sqrt3/4)`

`= (3sqrt3)/4`ab