Advertisements
Advertisements
Question
If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Solution
Let r1, r2 and 01, 02 be the radii and angles subtended at the centre of two circles, respectively.
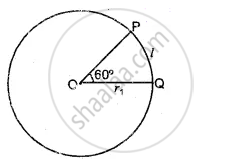
Let its radius = r1
l = r1θ1
= r1 `pi/3`
∴ r1 = `(3l)/pi` …(i)
For the second circle,
Let radius = r2
Arc length = l
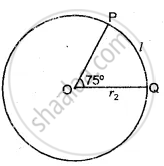
The angle made by the arc at the centre, θ2 = 75°
= `75 xx π/180` radians
= `(5π)/12` radians
r2 = `(12l)/(5π)`
On dividing equation (i) by equation (ii)
`r^1/r^2 = (3l)/π + (12l)/(5π)`
= `(3l)/πxx(5π)/(12l)` = 5 : 4.
APPEARS IN
RELATED QUESTIONS
Find the radian measure corresponding to the following degree measure:
– 47° 30'
Find the radian measure corresponding to the following degree measure:
240°
Find the degree measure corresponding to the following radian measure `(use pi = 22/7)`
`11/16`
Find the degree measures corresponding to the following radian measures (Use `pi = 22/7`)
`(5pi)/3`
Find the degree measure corresponding to the following radian measure (use `pi= 22/7`).
`(7pi)/6`
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
10 cm
Find the degree measure corresponding to the following radian measure:
\[- \frac{5\pi}{6}\]
Find the degree measure corresponding to the following radian measure:
(−3)c
Find the degree measure corresponding to the following radian measure:
1c
Find the radian measure corresponding to the following degree measure:
300°
Find the radian measure corresponding to the following degree measure: 125° 30'
One angle of a triangle \[\frac{2}{3}\] x grades and another is \[\frac{3}{2}\] x degrees while the third is \[\frac{\pi x}{75}\] radians. Express all the angles in degrees.
Find the magnitude, in radians and degrees, of the interior angle of a regular pentagon.
Find the magnitude, in radians and degrees, of the interior angle of a regular octagon.
Find the magnitude, in radians and degrees, of the interior angle of a regular duodecagon.
The angles of a triangle are in A.P. and the number of degrees in the least angle is to the number of degrees in the mean angle as 1 : 120. Find the angles in radians.
Find the length which at a distance of 5280 m will subtend an angle of 1' at the eye.
A wheel makes 360 revolutions per minute. Through how many radians does it turn in 1 second?
The radius of a circle is 30 cm. Find the length of an arc of this circle, if the length of the chord of the arc is 30 cm.
Find the distance from the eye at which a coin of 2 cm diameter should be held so as to conceal the full moon whose angular diameter is 31'.
If the arcs of the same length in two circles subtend angles 65° and 110° at the centre, find the ratio of their radii.
Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm.
If the angles of a triangle are in A.P., then the measures of one of the angles in radians is
The angle between the minute and hour hands of a clock at 8:30 is
At 3:40, the hour and minute hands of a clock are inclined at
If the arcs of the same length in two circles subtend angles 65° and 110° at the centre, than the ratio of the radii of the circles is
The radius of the circle whose arc of length 15 π cm makes an angle of \[\frac{3\pi}{4}\] radian at the centre is
Find the value of `sqrt(3)` cosec 20° – sec 20°
Find the value of tan 9° – tan 27° – tan 63° + tan 81°
Prove that `(sec8 theta - 1)/(sec4 theta - 1) = (tan8 theta)/(tan2 theta)`
“The inequality `2^sintheta + 2^costheta ≥ 2^(1/sqrt(2))` holds for all real values of θ”
The value of tan1° tan2° tan3° ... tan89° is ______.
State whether the statement is True or False? Also give justification.
One value of θ which satisfies the equation sin4θ - 2sin2θ - 1 lies between 0 and 2π.
