Advertisements
Advertisements
Question
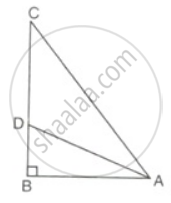
In the given figure; ∠C = 90o and D is mid-point of AC.
Find :
(i) `(tan∠CAB)/ (tan∠CDB)` (ii) `(tan∠ABC)/ (tan∠DBC)`
Solution
Since D is mid-point of AC so AC = 2DC
(i) `(tan∠CAB)/ (tan∠CDB)`
= `("BC"/"AC")/("BC"/"DC")`
= `"BC"/"2 DC"."DC"/"BC"`
= `(1)/(2)`
(ii) `(tan∠ABC)/ (tan∠DBC)`
= `("AC"/"BC")/("DC"/"BC")`
= `"2 DC"/"BC"."BC"/"DC"`
= 2
APPEARS IN
RELATED QUESTIONS
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of Sin A cos C + Cos A Sin C
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
If tan θ = `20/21` show that `((1-sin θ + cos θ))/((1+ sin θ +cos θ)) = 3/7`
Evaluate:
`(5 cos^2 60^circ + 4 sec^2 30^circ - tan^2 45^circ)/(sin^2 30^circ + cos^2 30^circ)`
Form the following figure, find the values of:
- cos B
- tan C
- sin2B + cos2B
- sin B. cos C + cos B. sin C

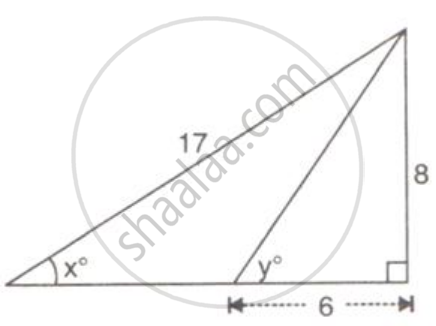
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
In the given figure, ΔABC is right angled at B.AD divides BC in the ratio 1 : 2. Find
(i) `("tan"∠"BAC")/("tan"∠"BAD")` (ii) `("cot"∠"BAC")/("cot"∠"BAD")`