Advertisements
Advertisements
Question
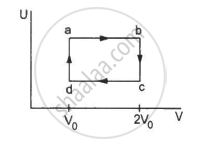
Refer to figure. Let ∆U1 and ∆U2 be the change in internal energy in processes A and B respectively, ∆Q be the net heat given to the system in process A + B and ∆W be the net work done by the system in the process A + B.

(a) ∆U1 + ∆U2 = 0
(b) ∆U1 − ∆U2 = 0
(c) ∆Q − ∆W = 0
(d) ∆Q + ∆W = 0
Solution
(a) ∆U1 + ∆U2 = 0
(c) ∆Q − ∆W = 0
The process that takes place through A and returns back to the same state through B is cyclic. Being a state function, net change in internal energy, ∆U will be zero, i.e.
∆U1 (Change in internal energy in process A) = ∆U2 (Change in internal energy in process B)
\[\Rightarrow \Delta U = \Delta U_1 + \Delta U_2 = 0\]
Here, ∆U is the total change in internal energy in the cyclic process.
Using the first law of thermodynamics, we get
\[\Delta Q - \Delta W = \Delta U\]
Here, ∆Q is the net heat given to the system in process A + B and ∆W is the net work done by the system in the process A + B.
Thus,
∆Q - ∆W = 0
APPEARS IN
RELATED QUESTIONS
An electric heater supplies heat to a system at a rate of 100W. If the system performs work at a rate of 75 Joules per second. At what rate is the internal energy increasing?
Write the mathematical expression of the First Law of Thermodynamics for the Isobaric process.
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
Calculate the increase in the internal energy of 10 g of water when it is heated from 0°C to 100°C and converted into steam at 100 kPa. The density of steam = 0.6 kg m−3. Specific heat capacity of water = 4200 J kg−1 °C−1 and the latent heat of vaporization of water = 2.25 × 10 6J kg−1.
Choose the correct option.
Which of the following is an example of the first law of thermodynamics?
For an Isothermal process
Define an isolated system.
A sample of gas absorbs 4000 kJ of heat and surrounding does 2000 J of work on sample. What is the value of ∆U?
In a given process for an ideal gas, dW = 0 and dQ < 0. Then for the gas ____________.
The initial state of a certain gas is (Pi, Vi, Ti). It undergoes expansion till its volume becomes Vf. Consider the following two cases:
- the expansion takes place at constant temperature.
- the expansion takes place at constant pressure.
Plot the P-V diagram for each case. In which of the two cases, is the work done by the gas more?
Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in figure.
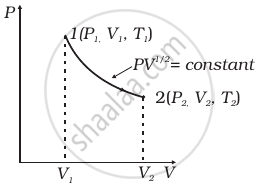
- Find the work done when the gas is taken from state 1 to state 2.
- What is the ratio of temperature T1/T2, if V2 = 2V1?
- Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2 = 2V1.
An ideal gas is taken through series of changes ABCA. The amount of work involved in the cycle is ______.
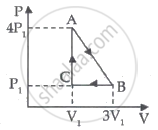
ΔU = 0 is true for ______.
An ideal gas (γ = 1.5) is expanded adiabatically. How many times has the gas had to be expanded to reduce the root mean square velocity of molecules two times?
An ideal gas having pressure p, volume V and temperature T undergoes a thermodynamic process in which dW = 0 and dQ < 0. Then, for the gas ______.
104 J of work is done on a certain volume of a gas. If the gas releases 125 kJ of heat, calculate the change in internal energy of the gas.
In an adiabatic process, ______.
Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R.
Obtain an expression for the workdone by a gas in an isothermal process.
Define isochoric process
