Advertisements
Advertisements
Question
Sum of the first p, q and r terms of an A.P. are a, b and c, respectively.
Prove that `a/p (q - r) + b/q (r- p) + c/r (p - q) = 0`
Solution
Let a1 and d be the first term and the common difference of the A.P. respectively.
According to the given information

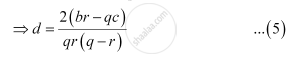
Equating both the values of d obtained in (4) and (5), we obtain
aq - bppqp - q = br - qcqrq - r⇒aq - bppp - q = br - qcrq - r⇒rq - raq - bp = pp - qbr - qc⇒raq - bpq - r = pbr - qcp - q⇒aqr - bprq - r = bpr - cpqp - q
Dividing both sides by pqr, we obtain

APPEARS IN
RELATED QUESTIONS
How many terms of the A.P. -6 , `-11/2` , -5... are needed to give the sum –25?
Show that the sum of (m + n)th and (m – n)th terms of an A.P. is equal to twice the mth term.
if `a(1/b + 1/c), b(1/c+1/a), c(1/a+1/b)` are in A.P., prove that a, b, c are in A.P.
A farmer buys a used tractor for Rs 12000. He pays Rs 6000 cash and agrees to pay the balance in annual installments of Rs 500 plus 12% interest on the unpaid amount. How much will be the tractor cost him?
Let < an > be a sequence. Write the first five term in the following:
a1 = 1, an = an − 1 + 2, n ≥ 2
Show that the following sequence is an A.P. Also find the common difference and write 3 more terms in case.
9, 7, 5, 3, ...
If the sequence < an > is an A.P., show that am +n +am − n = 2am.
Which term of the A.P. 84, 80, 76, ... is 0?
Is 68 a term of the A.P. 7, 10, 13, ...?
Is 302 a term of the A.P. 3, 8, 13, ...?
Which term of the sequence 12 + 8i, 11 + 6i, 10 + 4i, ... is purely real ?
How many terms are there in the A.P. 7, 10, 13, ... 43 ?
If 9th term of an A.P. is zero, prove that its 29th term is double the 19th term.
If 10 times the 10th term of an A.P. is equal to 15 times the 15th term, show that 25th term of the A.P. is zero.
The 4th term of an A.P. is three times the first and the 7th term exceeds twice the third term by 1. Find the first term and the common difference.
The first and the last terms of an A.P. are a and l respectively. Show that the sum of nthterm from the beginning and nth term from the end is a + l.
If the sum of three numbers in A.P. is 24 and their product is 440, find the numbers.
The angles of a quadrilateral are in A.P. whose common difference is 10°. Find the angles.
Find the sum of all integers between 84 and 719, which are multiples of 5.
If 12th term of an A.P. is −13 and the sum of the first four terms is 24, what is the sum of first 10 terms?
If the 5th and 12th terms of an A.P. are 30 and 65 respectively, what is the sum of first 20 terms?
Find the sum of odd integers from 1 to 2001.
If \[\frac{b + c}{a}, \frac{c + a}{b}, \frac{a + b}{c}\] are in A.P., prove that:
bc, ca, ab are in A.P.
If \[a\left( \frac{1}{b} + \frac{1}{c} \right), b\left( \frac{1}{c} + \frac{1}{a} \right), c\left( \frac{1}{a} + \frac{1}{b} \right)\] are in A.P., prove that a, b, c are in A.P.
There are 25 trees at equal distances of 5 metres in a line with a well, the distance of the well from the nearest tree being 10 metres. A gardener waters all the trees separately starting from the well and he returns to the well after watering each tree to get water for the next. Find the total distance the gardener will cover in order to water all the trees.
A man starts repaying a loan as first instalment of Rs 100 = 00. If he increases the instalments by Rs 5 every month, what amount he will pay in the 30th instalment?
Write the value of n for which n th terms of the A.P.s 3, 10, 17, ... and 63, 65, 67, .... are equal.
If \[\frac{3 + 5 + 7 + . . . + \text { upto n terms }}{5 + 8 + 11 + . . . . \text { upto 10 terms }}\] 7, then find the value of n.
In the arithmetic progression whose common difference is non-zero, the sum of first 3 n terms is equal to the sum of next n terms. Then the ratio of the sum of the first 2 n terms to the next 2 nterms is
If four numbers in A.P. are such that their sum is 50 and the greatest number is 4 times the least, then the numbers are
Let Sn denote the sum of n terms of an A.P. whose first term is a. If the common difference d is given by d = Sn − k Sn − 1 + Sn − 2 , then k =
If the first, second and last term of an A.P are a, b and 2a respectively, then its sum is
If a, b, c are in G.P. and a1/x = b1/y = c1/z, then xyz are in
The product of three numbers in A.P. is 224, and the largest number is 7 times the smallest. Find the numbers
Find the rth term of an A.P. sum of whose first n terms is 2n + 3n2
The sum of terms equidistant from the beginning and end in an A.P. is equal to ______.
The number of terms in an A.P. is even; the sum of the odd terms in lt is 24 and that the even terms is 30. If the last term exceeds the first term by `10 1/2`, then the number of terms in the A.P. is ______.
