Advertisements
Advertisements
प्रश्न
Sum of the first p, q and r terms of an A.P. are a, b and c, respectively.
Prove that `a/p (q - r) + b/q (r- p) + c/r (p - q) = 0`
उत्तर
Let a1 and d be the first term and the common difference of the A.P. respectively.
According to the given information

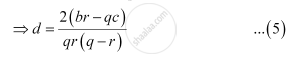
Equating both the values of d obtained in (4) and (5), we obtain
aq - bppqp - q = br - qcqrq - r⇒aq - bppp - q = br - qcrq - r⇒rq - raq - bp = pp - qbr - qc⇒raq - bpq - r = pbr - qcp - q⇒aqr - bprq - r = bpr - cpqp - q
Dividing both sides by pqr, we obtain

APPEARS IN
संबंधित प्रश्न
How many terms of the A.P. -6 , `-11/2` , -5... are needed to give the sum –25?
If the sum of a certain number of terms of the A.P. 25, 22, 19, … is 116. Find the last term
If the sum of n terms of an A.P. is (pn + qn2), where p and q are constants, find the common difference.
If the sum of first p terms of an A.P. is equal to the sum of the first q terms, then find the sum of the first (p + q) terms.
The pth, qth and rth terms of an A.P. are a, b, c respectively. Show that (q – r )a + (r – p )b + (p – q )c = 0
A person writes a letter to four of his friends. He asks each one of them to copy the letter and mail to four different persons with instruction that they move the chain similarly. Assuming that the chain is not broken and that it costs 50 paise to mail one letter. Find the amount spent on the postage when 8th set of letter is mailed.
A man deposited Rs 10000 in a bank at the rate of 5% simple interest annually. Find the amount in 15th year since he deposited the amount and also calculate the total amount after 20 years.
A manufacturer reckons that the value of a machine, which costs him Rs 15625, will depreciate each year by 20%. Find the estimated value at the end of 5 years.
How many terms are there in the A.P.\[- 1, - \frac{5}{6}, -\frac{2}{3}, - \frac{1}{2}, . . . , \frac{10}{3}?\]
In a certain A.P. the 24th term is twice the 10th term. Prove that the 72nd term is twice the 34th term.
Find the 12th term from the following arithmetic progression:
1, 4, 7, 10, ..., 88
The sum of 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms is 34. Find the first term and the common difference of the A.P.
Three numbers are in A.P. If the sum of these numbers be 27 and the product 648, find the numbers.
Find the sum of the following arithmetic progression :
\[\frac{x - y}{x + y}, \frac{3x - 2y}{x + y}, \frac{5x - 3y}{x + y}\], ... to n terms.
Find the sum of all odd numbers between 100 and 200.
Find the sum of all integers between 50 and 500 which are divisible by 7.
Find the sum of all integers between 100 and 550, which are divisible by 9.
Find the sum of all those integers between 100 and 800 each of which on division by 16 leaves the remainder 7.
Find the r th term of an A.P., the sum of whose first n terms is 3n2 + 2n.
In an A.P. the first term is 2 and the sum of the first five terms is one fourth of the next five terms. Show that 20th term is −112.
If the sum of n terms of an A.P. is nP + \[\frac{1}{2}\] n (n − 1) Q, where P and Q are constants, find the common difference.
If \[\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\] are in A.P., prove that:
\[\frac{b + c}{a}, \frac{c + a}{b}, \frac{a + b}{c}\] are in A.P.
If a, b, c is in A.P., then show that:
bc − a2, ca − b2, ab − c2 are in A.P.
In a cricket team tournament 16 teams participated. A sum of ₹8000 is to be awarded among themselves as prize money. If the last place team is awarded ₹275 in prize money and the award increases by the same amount for successive finishing places, then how much amount will the first place team receive?
If the sums of n terms of two arithmetic progressions are in the ratio 2n + 5 : 3n + 4, then write the ratio of their m th terms.
Write the sum of first n odd natural numbers.
Write the value of n for which n th terms of the A.P.s 3, 10, 17, ... and 63, 65, 67, .... are equal.
If the sums of n terms of two AP.'s are in the ratio (3n + 2) : (2n + 3), then find the ratio of their 12th terms.
If 7th and 13th terms of an A.P. be 34 and 64 respectively, then its 18th term is
Sum of all two digit numbers which when divided by 4 yield unity as remainder is
If Sn denotes the sum of first n terms of an A.P. < an > such that
Let Sn denote the sum of n terms of an A.P. whose first term is a. If the common difference d is given by d = Sn − k Sn − 1 + Sn − 2 , then k =
Mark the correct alternative in the following question:
If in an A.P., the pth term is q and (p + q)th term is zero, then the qth term is
If the sum of m terms of an A.P. is equal to the sum of either the next n terms or the next p terms, then prove that `(m + n) (1/m - 1/p) = (m + p) (1/m - 1/n)`
A man saved Rs 66000 in 20 years. In each succeeding year after the first year he saved Rs 200 more than what he saved in the previous year. How much did he save in the first year?
If the sum of n terms of a sequence is quadratic expression then it always represents an A.P
If a1, a2, a3, .......... are an A.P. such that a1 + a5 + a10 + a15 + a20 + a24 = 225, then a1 + a2 + a3 + ...... + a23 + a24 is equal to ______.
If b2, a2, c2 are in A.P., then `1/(a + b), 1/(b + c), 1/(c + a)` will be in ______
