Advertisements
Advertisements
Question
Verify cos3A = 4cos3A – 3cosA, when A = 30°
Solution
L.H.S = cos3A
= cos3(30°)
= cos90°
= 0
R.H.S = 4cos3A – 3cosA
= 4cos330° – 3cos30°
=`4(sqrt(3)/2)^3 - 3(sqrt(3)/2)`
= `(4 xx 3sqrt(3))/8 - (3sqrt(3))/2`
= `(3sqrt(3))/2 - (3sqrt(3))/2`
= 0
∴ L.H.S = R.H.S
Hence it is proved.
APPEARS IN
RELATED QUESTIONS
Evaluate the following
`sec 11^@/(cosec 79^@)`
Evaluate: `sin 50^@/cos 40^@ + (cosec 40^@)/sec 50^@ - 4 cos 50^@ cosec 40^@`
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios: sin 45°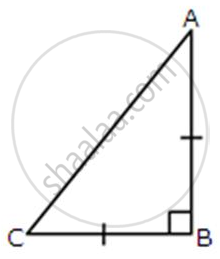
If sin x = cos y, then x + y = 45° ; write true of false
find the value of :
`( tan 45°)/ (cos ec30°) +( sec60°)/(co 45°) – (5 sin 90°)/ (2 cos 0°)`
If A = 30°;
show that:
`(1 – cos 2"A")/(sin 2"A") = tan"A"`
Prove that : cos60° . cos30° - sin60° . sin30° = 0
Find the value of x in the following: 2 sin3x = `sqrt(3)`
The value of 5 sin2 90° – 2 cos2 0° is ______.
Evaluate: `(5 "cosec"^2 30^circ - cos 90^circ)/(4 tan^2 60^circ)`
